Le contexte géométrique.

...Une sphère est un espace de dimension 2. Il faut deux paramètres pour y repérer un point. C'est un espace qui a une topologie (pour plus de détails sur la signification du mot topologie, voir ma bande dessinée le Topologicon, Ed. Belin). Une sphère n'a pas la même topologie, la même "forme" qu'un tore. La sphère possède des géodésiques. On peut y inscrire un trajet reliant deux points M₁ et M₂ et mesurer la longueur s parcourue. Cette longueur est indépendante des coordonnées choisies pour repérer les points, de même que les courbes géodésiques qui peuplent la surface.

...Joignons le centre de cette sphère à tous ses points. Nous obtenons une infinité de demi-droites. Celles-ci peuvent être repérées avec le même système de repérage que les points, par exemple deux angles q et j.

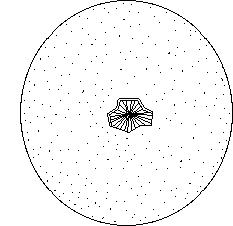
Ci-dessus notre sphère. On a fait un trou pour montrer l'ensemble des rayons vecteurs.

Enlevons maintenant la sphère et ne conservons plus que les rayons vecteurs.

...On a tronqué ces demi-droites, mais en fait, elles sont infinies. Chacune n'est définie que par la donné de deux paramètres, par exemple deux angles. La structure métrique a disparu. Plus de géodésiques, plus de longueurs. Qu'est-ce qui reste ?

- Toute demi-droite a un voisinage. On peut sélectionner des demi-droites voisines pour enserrer celle-ci dans une sorte de cône. A l'intérieur de ce cône on peut en faire figurer un plus étroit, qui contient la demi-droite. C'est l'affaire des cercles concentriques ou des poupées russes, mais avec des faisceaux de demi-droites. Mais il ne s'agit pas de tracer des géodésiques sur ces cônes-là. Chacune de leurs génératrices sont simplement un ensemble de deux paramètres, par exemple deux angles.

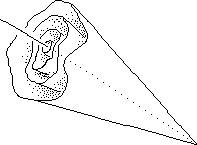
- On distingue une idée intuitive de différentiabilité . Il n'y a pas de discontinuité dans cette "texture"-là.

Prenons une surface plane, avec géodésiques, longueur etc...

...Quel que soit le système de coordonnées que je choisis je devrai toujours repérer la position de mes points avec deux nombres réels (x,y), (r,q) etc...

Ces nombres réels sont pris dans R2, c'est à dire dans l'ensemble des couples de nombres réels, comme (3,8705 , - 17,56). Tout couple de points pris dans cet espace des couples de nombres réels a un voisinage. C'est "continu".

Ces objets "pré-métriques" sont appelés variétés (les mathématiciens ont le chic pour choisir des mots qui n'ont aucun pouvoir évocateur pour l'homme de la rue ).

...A ce stade on peut donc sauter ce pas qui consiste à considérer un ensemble de n réels (espace à n dimensions), sans lui attacher automatiquement d'idée de longueur ou de géodésiques.

...C'est un peu comme si on considérait une surface dont les points n'auraient pour contrainte que de garder le contact avec leurs voisins. Elle serait infiniment élastique et déformable. Par convention, si nous représentons une surface par son contour (soit son bord, soit son contour apparent, on évoquera ce concept "mouvant" de variété en enlevant simplement le contour :

...Cette image évoque d'ailleurs l'ombre de l'objet. Et une ombre n'a ni consistance, ni forme. Sa géométrie dépend de l'objet sur lequel elle se projette.

On peut aussi se représenter la variété (en anglais manifold) , sans sa métrique, comme une famille de droites.

 
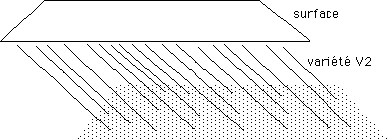
...Là, on a mis des droites qui ont l'air parallèle. Il faudrait que ces droites soient... n'importe comment, tout en conservant leurs relations de proximité, de voisinage.

...Finalement, une bonne image d'une variété V2, c'est un paquet de spaghettis qu'on fait d'abord cuire, puis qu'on peut plier et tordre en tous sens, mais sans modifier l'ordonnance des pâtes les unes par rapport aux autres.

Toujours est-il qu'on peut effectuer sur une variété une opération de revêtement à deux feuillets, qu'on munit de métriques, suggérée par l'image ci-après :

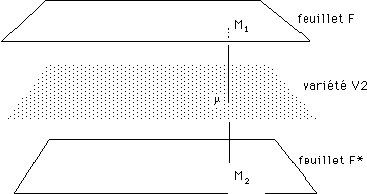
Ici deux feuillets 2d dotés de métriques identiques (euclidiennes). Mais on peut tout aussi bien faire :

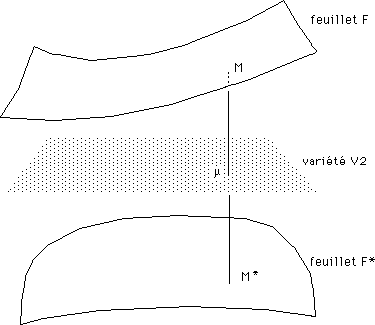
...On appelera M et M* des points conjugués . Le fait de dire que les deux espaces conjugués sont construits comme le revêtement à deux feuillets d'une variété signifie simplement qu'il existe une correspondance point à point entre les deux feuillets F et F*, mais, par exemple, les distances entre des couples de points homologues (M₁,M₂) , (M*₁, M*₂) peuvent être différentes. La seule contrainte est finalement que les voisinages de points se correspondent également et qu'à toute région non singulière d'une nappe correspond une région également non singulière.

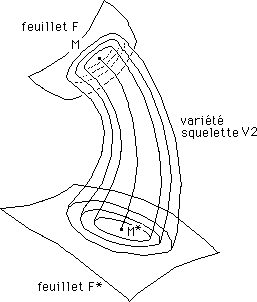
...On retrouve le paquet de nouilles flexibles de tout à l'heure. La structure de "variété-squelette " n'est là que pour construire l'application injective entre les deux objets géométriques. Le dessin ci-dessus est destiné à faire complètement éclater des questions comme "comment les feuillets F et F* sont-ils disposés l'un par rapport à l'autre ? Si F est un univers, où est F* ? ". Ces feuillets sont simplement conjugués, avec une correspondance point par point et ces points conjugués peuvent être décrits par les mêmes coordonnées.

 Sommaire article      Sommaire Science       Page d'Accueil

Retour vers Guide-Sciences

Nombre de consultations de cette page depuis le 1° juillet 2004 :