Courbures conjuguées.

...Comment appréhender l'idée de courbure locale, positive ou négative, dans un espace à trois dimensions. Prenons une sphère. Plantons un clou quelque part. Attachons-y une ficelle de longueur L et fixons à l'autre extrémité un crayon. Nous allons pouvoir tracer un cercle, qui sera un parallèle. Effectuons la même opération avec un plan et une selle de cheval.

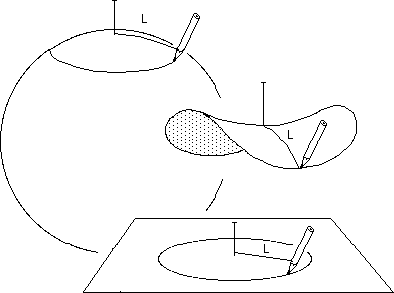
...Sur un plan le périmètre est 2 p L et la surface du disque p L².

...Sur la sphère le périmètre et l'aire de la calotte sont plus petits. Sur une selle de cheval le périmètre et l'aire délimitée par cette courbe fermée sont plus grands. Exemple : si on prend une sphère de rayon R et une longueur L égale au quart du périmètre équatorial, soit p R/2 :

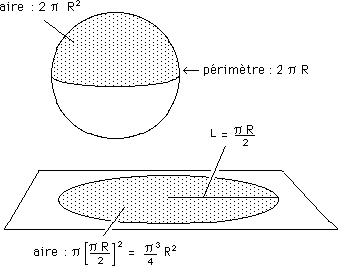
...L'aire du disque est 3,875 fois plus grande que l'aire de la calotte sphérique. Son périmètre est 1,57 fois plus grand que l'équateur.
 

...En effectuant des mesures analogues sur une surface on peut savoir si la courbure locale est positive ou négative. Situation analogue en 3d. On prend alors un point, une ficelle de rayon L et on trace... une sphère. Si l'aire de cette sphère est plus petite que l'aire euclidienne 4 p L² on en concluera que la courbure locale est positive Si cette aire est plus petite que l'aire euclidienne 4 p L² on en concluera que la courbure locale est négative. Même conclusion pour le volume. Contentons-nous de ces idées qualitatives . En trois et quatre dimension on peut définir une longueur R, dite courbure scalaire , qui se calcule à partir d'un tenseur de courbure.

...Dans le modèle cosmologique que nous présentons, on décide de conjuguer deux feuillets d'univers tels que les valeurs des courbures scalaires locales en des points conjugués soient inverses :

...C'est la façon purement géométrique d'envisager les choses. Il est alors aisé d'en donner une image didactique 2d, modulo les réserves d'usage quand à la portée réelle de telles représentations. C'est le dessin de la figure ci-après :

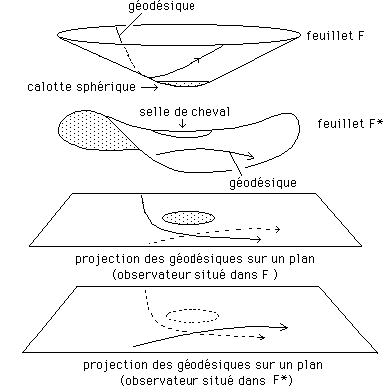
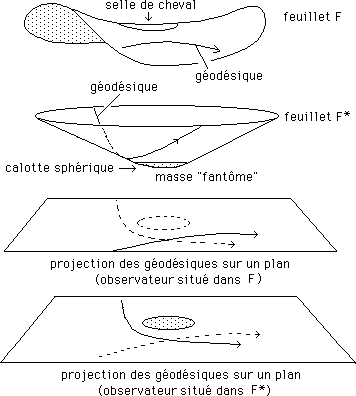
En haut, un posicône émoussé. La courbure locale est nulle sur le tronc de cône et positive dans la calotte sphérique.

En bas un "négacône émoussé". La courbure est nulle sur le tronc de négacône et négative dans la selle de cheval.

...On a projeté l'objet et les géodésiques sur deux plans-espaces de représentation euclidiens. Le premier est celui d'un observateur physiquement situé dans le feuillet F, qui pourra ainsi voir l'objet massif, mais pas la particule-témoins cheminant dans le feuillet F*.
 

...L'invisibilité d'un objet situé dans un feuillet par un observateur situé dans l'autre est de nature purement géométrique. On suppose que les photons suivent des géodésiques (particulières) de chaque feuillet. Des photons j cheminent dans le feuillet F (notre feuillet d'univers) et des photons j* , qu'on pourra appeler "photons fantômes" (ghost photons) chemine dans le feuillet F*, le "feuillet fantôme" (ghost universe). Le fait que les deux feuillets forment un ensemble disjoint, non-connexe interdit à tout photon d'un feuillet de passer sur l'autre.

...Le "fonctionnement" d'un tel système géométrique est moins compliqué qu'il n'y paraît.

...Le feuillet F a sa géométrie, qui est entièrement décrite par une "métrique" g , à partir de laquelle on construit son système de géodésiques. A partir de cette métrique g on peut construire un tenseur géométrique S et l'identifier à un tenseur T , qui soit "source du champ", origine de cette courbure, en écrivant l'équation d'Einstein :

La géométrie du second feuillet, telle que sa courbure scalaire soit inverse, correspond à une métrique g* , à partir de laquelle on peut construire un tenseur géométrique S*. L'inversion de courbure découle simplement de :

...Considérons une géodésique du feuillet F et faisons figurer la courbe correspondant aux points conjugués, dans l'autre feuillet. Ca n'est pas une géodésique de celui-ci.

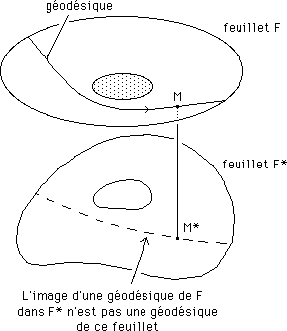
Inversement :

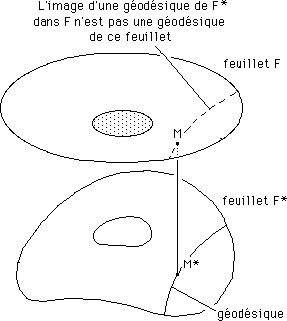
...A ce stade, où en sommes-nous ? Nous avons doté l'univers (supposé être le feuillet F, notre propre espace-temps) d'un frère jumeau. La matière présente dans notre univers (le tenseur T) détermine sa géométrie, mais elle détermine également celle du jumeau. Nous supposons que notre univers contient uniquement des masses positives et, plus généralement, des particules possédant des énergies positives. Nous n'envisageons pas la présence possible de masses négative dans notre feuillet d'espace-temps. Le tenseur T est donc soit positif, là où il y a de l'énergie-matière, soit nul là où règne un vide poussé. La courbure locale de F est donc soit nulle, soit positive, mais ne peut être négative.

...Par contre la courbure du feuillet F* (on parlera alors de courbure induite) est soit nulle, soit négative.

...S'il existe des particules dans ce feuillet, nous supposons qu'elle suivent aussi des géodésiques de celui-ci. Or que constatons-nous en regardant la figure ci-dessus ? L'objet grisé, cette masse présente dans notre univers, dans le feuillet F, se comporte comme un objet répulsif (voir la courbure de la trajectoire-géodésique) dans le feuillet F*.

...Nous avons construit une solution mathématique exacte correspondant à ce couple de "métriques conjuguées" (g , g*). [Voir dans le site: papier Geometrical Physics B], . La solution g est identique à ce que nous avons appelé les métriques de Schwarzschild extérieure (à l'extérieur de l'astre) et intérieure (dans l'astre lui-même). Nous proposons d'appeler la seconde métrique "Anti-Schwarzschild". [Voir dans le site: Geometrical Physics A, 7, le papier 2 : Conjugated steady state metrics. Exact solutions. ]
 

Avec de la "matière fantôme".

Dans cette optique de géométries conjuguées, on peut inverser la situation et supposer qu'une masse (positive) se trouve présente quelque part dans le feuillet F*. Elle y crée alors une courbure positive et l'image didactique 2d de cette géométrie correspond au cône émoussé, à une solution de Schwarzschild, mais dans le feuillet F*.

...Même remarque pour la façon dont les observateurs de différents feuillets perçoivent l'effet de cette masse sur une particule-témoins cheminant dans leur univers.

...L'examen du schéma ci-dessus nous permet de dégager les lois d'interaction entre la matière et la matière fantôme (ghost-matter), localisée dans le second univers le ghost universe.

- Deux particules de matière s'attirent

- Deux particules de matière-fantôme s'attirent.

- Matière et matière fantôme se repoussent.

...On voit que c'est différent du schéma suggéré par Souriau, selon lequel le particules de la seconde espèce, non seulement repoussaient celles constituant notre matière, mais se repoussaient entre elles.

...La seconde géométrie correspond à la présence de masses positives m*, dans le feuillet F*. On pourra y définir une densité de matière matière r* > 0 (ou plus précisément de ghost energy-matter, puisque le second feuillet, le ghost universe, contient aussi du "rayonnement fantôme", des ghost photons et des ghost neutrinos). L'énergie des ghost particles est positive, de même que la pression p*.

...A partir de ces grandeurs on peut construire un tenseur d'énergie-matière fantôme T* (le tenseur énergie matière le plus général est un peu plus que cela, mais cette description schématique suffit "pour les besoins usuels").

L'équation de champ donnant la géométrie dans le feuillet F* est :

 
...Ce sont les deux équations de tout à l'heure, inversées. Dans le feuillet F la géométrie est induite , au sens où elle est créée par de la matière M* située dans F* et donc invisible depuis le feuillet F.

 
...On peut maintenant envisager que le deux feuillets soient peuplés chacun par leur propre matière, de densités r et r*.

Les métriques conjuguées se déduisent alors du système d'équations :

ou :

elle est alors négative dans la région adjacente , conjuguée, du feuillet F*.

Si la courbure est localement négative dans le feuillet F c'est que :

ou :

elle est alors positive dans la région adjacente , conjuguée, du feuillet F*.

Si la courbure est nulle dans une région du feuillet F, elle également nulle dans le feuillet F*, ce qui signifiera soit que :

soit que :

Newton et anti-Newton.

La loi de Newton se déduit de l'équation d'Einstein en supposant :

- Que la courbure locale est faible

- Que les vitesses sont faibles devant la vitesse de la lumière

- Que le système est "quasi-stationnaire" (cosmologiquement parlant).

...Elle se déduit de la même manière du système d'équations de champ couplées présenté plus haut. Voir :
J.P.Petit and P.Midy : Matter ghost matter astrophysics. 1 : The geometrical framework. The matter era and Newtonian approximation. [voir sur le site: Geometrical Physics A , 4 , 1998, section 4. ]

On a donc la dynamique ci-après :

- Deux particules de matière m₁ et m₂ s'attirent selon la loi de Newton.

- Deux particules de ghost matter, de "matière-fantôme" m*₁ et m*₂ s'attirent selon la loi de Newton.

- Deux particules m et m*, appartenant à de feuillets différents se repoussent selon "anti-Newton".

A propos des tests de la Relativité Générale.

...Le modèle n'est pas en contradiction avec ceux-ci. En effet, comme la matière et la ghost matter se repoussent, là où il y a une concentration de matière (par exemple notre galaxie), dans la portion adjacente, conjuguée du ghost universe, règne un vide poussé : la matière y a fait le ménage en repoussant les masses fantômes au loin.

Dans le voisinage du soleil le tenseur T* (ghost matter) est donc négligeable devant T (matière) et l'équation de champ devient :

...Dans le papier : "J.P.Petit and P.Midy : Geometrization of antimatter through coadjoint action of a group on its momentum space. 3 : Twin group. Matter anti-matter duality in the ghost space. Reinterpretation of the CPT theorem. [Voir sur le site: Geometrical Physics B, 1-3 ], 1998.", la structure gémellaire est approchée différemment : à travers la théorie des groupes (groupe gémellaire). On verra en particulier que la dualité matière antimatière existe dans les deux feuillets. Dans le ghost universe il existe de la ghost matter et de l'anti-ghost matter.

...Nous connaissons l'approximation newtonienne. Nous pouvons donc faire des simulations numériques. Nous pouvons aussi tenter de construire des solutions analytiques. Nous devrons aussi, pour être complets, produire un modèle d'évolution cosmologique, qu'on appelera Twin Bang , puisqu'il affecte les deux univers. .