Espace de représentation.

...On avait vu qu'un cylindre était une surface développable. Prenez maintenant une feuille de papier. C'est une surface plane, euclidienne. Ses géodésiques sont des droites. Tracez quelques droites sur cette feuille, puis chiffonnez-la.

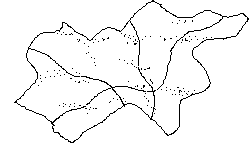
...Si vous pouviez rigidifier cette surface plane chiffonnée, vous vous apercevriez que cette opération n'a nullement modifié la distribution de ses géodésiques, que vous pourriez tracer de nouveau avec votre ruban adhésif. Vous avez simplement joué avec le mode de représentation de ce plan dans son espace de plongement tridimensionnel.

Une façon moins compliquée de procéder consiste à transformer une tôle en...tôle ondulée :

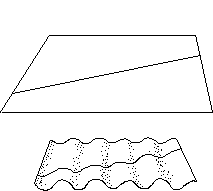
Géodésiques : inchangées.

...Les objets géométriques existent indépendamment de la façon dont nous nous les représentons, indépendamment de leur espace de représentation .

...Nous sommes censé habiter dans une "hypersurface quadridimensionnelle" : l'espace temps. La Relativité Générale consiste à essayer de construire sa géométrie, en tant que solution d'une équation de champ, puis à "lire" cette géométrie, en analysant les géodésiques de l'hypersurface. Il est évident qu'il n'est plus question alors d'espace de représentation. Pour ce faire il faudrait disposer d'une vision dans cinq dimensions, que nous ne possédons pas.

...En pratique, nous utilisons des coordonnées qui sont celles de l'espace euclidien, de projection. Imaginons que nous recherchions une solution géométrique propre à décrire l'espace temps au voisinage d'un corps massif et à l'intérieur de celui-ci. Nous allons supposer que le système possède la symétrie sphérique. De plus nous supposerons que ce système est stationnaire (ou quasi-stationnaire).

...Nous utiliserons alors les coordonnées sphériques (r , q , j) . En deux dimensions, nous n'en aurons que deux et notre symétrie sera circulaire. Nous utiliserons alors le système des coordonnées polaires du plan :

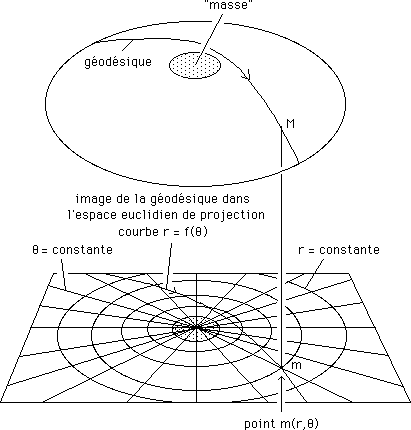
...Ce modèle du corps émoussé est une image didactique 2d d'une solution stationnaire qui existe effectivement en Relativité Générale et qui a été inventée par l'autrichien Schwarzschild, en 1917, en tant que solution particulière de "l'équation d'Einstein" :

déjà présentée plus haut. Cette solution est intelligente et subtile. Au plan calcul, elle n'est pas simple à construire. Cette précision pour tenter de dissiper un mythe : celui d'un Einstein, génie isolé dans le monde de son temps, peuplé d'ignorants.

...A partir de cette solution on montre alors qu'il existe, autour d'une masse possédant la symétrie sphérique des géodésiques planes , situées dans des plans, et on sait calculer leur forme : r = f (q). Ces trajectoires (ou du moins leur projection dans notre espace mental de représentation, euclidien) sont "quasi Keplériennes" et les lois de Kepler apparaissent alors comme une approximation, lorsque la masse qui crée cette géométrie (dans la vision newtonienne, cette "force") reste modérée, c'est à dire que la courbure locale, dans cette masse, reste faible.

...Cette solution est un des pivots de la Relativité Générale et, bien que cela ne puisse pas être évoqué par de simples images didactiques comme celles que nous offrons au lecteur, c'est elle qui permet de prévoir et de calculer par exemple l'avance du périhélie de Mercure. Einstein se servit de cette solution pour expliquer cet effet, déjà connu et récolta du même coup tous les lauriers de ce qu'on appela désormais "la théorie d'Einstein". Pourquoi Schwarzschild n'exploita-t-il pas lui-même sa découverte ? Parce qu'il tint absolument à s'engager et à partir sur les tranchées, où il fut gazé et mourut peu après.

...On n'est d'ailleurs pas très sûr que cette célèbre équation d'Einstein est bien de lui. Apparemment elle lui aurait été suggérée par le grand mathématicien Hilberth. Einstein n'accueillit pas non plus avec enthousiasme la découverte ultérieure du russe Friedmann, qui découvrit, lui, la solution instationnaire de l'équation de champ permettant de décrire l'évolution de l'univers. Même chose, en 1921 pour les travaux du jeune mathématicien Kaluza, dont les travaux, redécouverts, constituent maintenant le point de départ de la théorie des supercordes. Ces choses sont scientifiquement de peu d'intérêt et ne diminuent en rien la valeur d'Einstein, mais montrent que l'esprit sportif ne va pas forcément avec la valeur scientifique d'un individu.

Dans la solution développée par Schwarzschild, techniquement, l'espace est en deux parties. A l'intérieur de l'astre la densité de matière r est supposée constante. Le tenseur énergie-matière T, qui en dépend, est également non nul. A l'extérieur r et T sont nuls.

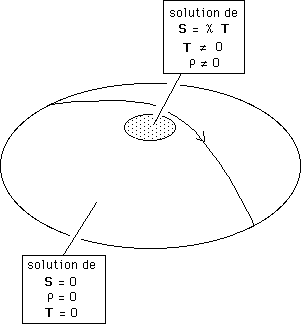
...Cette géométrie composite est donc solution de deux équations différentes, avec ou sans second membre. La densité de matière présente une discontinuité à la surface de l'astre (c'est également le cas pour le couple solution de Schwarzschild "intérieure" et solution de Schwarzschild "extérieure". Dans ce cas l'astre est une sphère de densité constante et celle-ci tombe brutalement à zéro à la surface de l'astre). Mais la continuité des géodésiques peut néanmoins être assurée, à travers des conditions mathématiques dont l'image a été donnée plus haut (raccord tronc de cône-calotte sphérique).

...Lorsque la masse devient importante et les effets de courbure prononcés, les trajectoires s'écartent alors plus nettement du modèle képlérien, par exemple au voisinage d'une étoile à neutrons. Ci-après l'avance du périhélie autour d'un tel astre (autour du soleil l'ellipse trajectoire de Mercure avance de 0,15 degré par siècle).

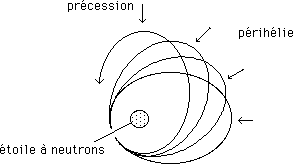
...La formule et le programme qui permettent de calculer ces trajectoires n'ont d'ailleurs rien de compliqué. Nous les donneront un jour sur ce site, pour les curieux.

...En ce moment nous posons quelques jalons géométriques en vue de discussions ultérieures, tout en rappelant que les modèles indiquées n'ont qu'un caractère indicatif. .