Eventuels problèmes posés par un choix de coordonnées.

...Nous allons évoquer les risques encourus en plaquant un système de coordonnées sur une solution géométrique, en exprimant cette solution dans ce système de coordonnées particulier : encore faut-il que celui-ci soit adéquat. Quand nous regardons la solution ci-dessus, en supposant que cette géométrie soit solution d'une équation de champ, le recours à un système de coordonnées (r , q) présupposait que la topologie était "localement sphérique", en deux dimensions, bien sûr. C'est à dire qu'à l'intérieur de tout cercle "centré sur ce centre géométrique hypothétique on pouvait toujours inscrire un cercle plus petit, jusqu'à ce que ce cercle devienne un point. Mathématiquement on dirait que tout cercle de rayon r délimite une "cellule contractile".

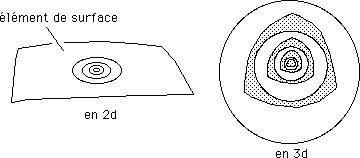
...En 3d, localement, l'univers serait "en poupées russes". A l'intérieur d'une sphère on pourrait toujours inscrire une sphère d'aire plus faible. En 3d, il s'agit d'une topologie localement sphérique.

Peut-il en être autrement ?

Oui, si la topologie de la surface est "localement torique". En 2d cela donne ceci :

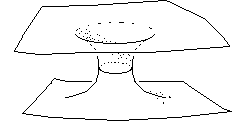
...Remarque : l'objet de la figureci-dessus est une surface 2d au sens où il faut deux paramètres pour y repérer la position d'un point. En ce sens une courbe est une "surface à une dimension". Quand il parlera du cercle, le géomètre emploiera l'expression "sphère S1", c'est à dire "sphère à une seule dimension" : il ne faut qu'un unique paramètre, l'abcisse, pour repérer un point sur une courbe, objet unidimensionnel. La sphère S2, la sphère "ordinaire" et le cercle, la sphère S1 on quelque chose en commun : ce sont des objets "fermés" (concept alors emprunté à la topologie).

...Ce nombre de quantités servant à définir la position d'un point dans un espace est précisément la définition de la dimension de cet espace. Ainsi considèrera-t-on l'espace temps (x,y,z,t) comme une hypersurface à quatre dimensions, parce qu'il faut quatre quantités pour y définir un point, dit "événement".

Fin de cette remarque sur le concept de dimension.

...Il faut bien garder une chose en tête. Le géomètre qui construit une solution particulière d'une équation de champ est aveugle, il ne peut pas voir l'objet géométrique qu'il obtient. Il ne peut que l'explorer, à travers ses géodésiques, en décrivant celles-ci dans un système de coordonnées particulières. Les coordonnées polaires de tout à l'heure correspondaient à l'intersection de la surface par une famille de cylindres coaxiaux :

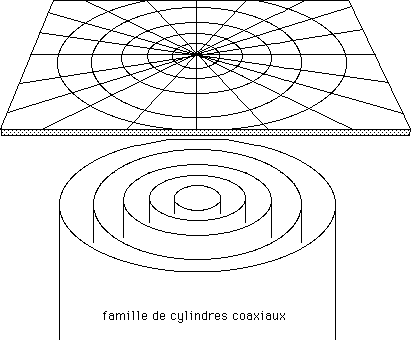
et par une famille de plans passant par l'axe commun de ceux-ci.

En 3d il s'agirait de l'intersection de l'espace par une famille de sphères concentriques.

 ...Mais que se passe-t-il si on coupe la surface présentant cette sorte de pont tubulaire par une famille de cylindres concentriques ? Tant que les cylindres coupent la surface, ça va. Mais quand leur périmètre devient inférieur à celui du "cercle de gorge" ces section deviennent des ... courbes imaginaires. Soit p le périmètre du cercle de gorge. Associons-le à une longueur R_g telle que p = 2 p R_g .

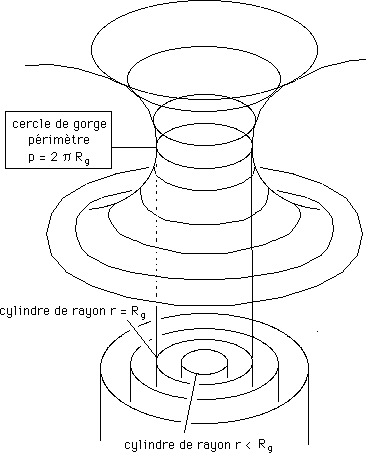
...Il est clair que tout cylindre de la famille tel que r < R_g ne coupe pas la surface. Lorsque le géomètre s'intéressera à l'allure des géodésiques de la surface pour r < R_g il trouvera des objets géométriques imaginaires.

...Quand on cherche l'intersection de deux points avec une droite, correspondant par exemple à x = xo on trouve deux valeurs réelles, pour y, lorsque la droite coupe effectivement le cercle. Sinon ces valeurs sont imaginaires pures.

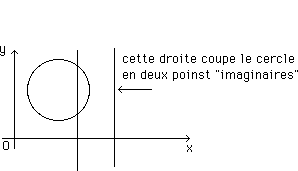
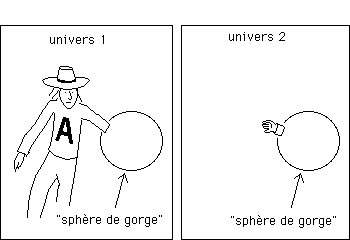
...Si un homme, qui explore une surface dans l'obscurité, sans pouvoir en percevoir la forme , qu'il ignore que la topologie de celle-ci est localement torique , il pourra être extrêmement déconcerté.
La surface peut être repérée à l'aide de deux familles de courbes :

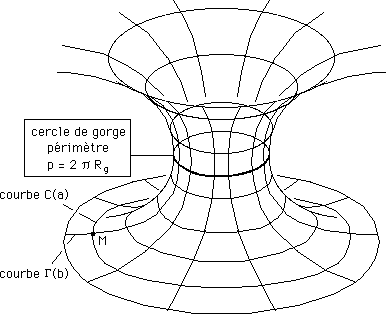
...Chaque courbe est définie par un paramètre. Un point M , à l'intersection de ces deux courbes, est bien défini par deux quantités (a,b), les deux valeurs des courbes passant par M.

...La première est constituée par des cercles qui ne sont pas des géodésiques de la surface (sauf le cercle de gorge), la seconde par des géodésiques, d'allure hyperbolique, orthogonales à ces cercles. Les courbes hyperboliques évoquent des trajectoires plongeantes, qui permettent de passer d'un nappe à une autre nappe.
On peut évidemment avoir la même situation pour une espace 3d, localement hypertorique. Les cercles seront remplacés par une famille de sphère, parmi lesquels on trouvera une sphère de gorge , d'aire minimale. Les lignes constituant les trajectoires orthogonales à cette famille de sphères constituent des trajectoires plongeantes permettant de passer par ce tunnel hypertorique et de réapparaître dans une autre nappe (ou feuillet) 3d.

...Cette remarque n'est pas gratuite. On aura l'occasion d'y revenir lorsqu'on mettra le modèle du trou noir en examen. En effet, dans ce modèle, lorsqu'on pénètre "à l'intérieur de la sphère horizon" la masse d'une particule devient... imaginaire pure (cela et bien d'autres choses encore). On est alors en droit de se demander si on est encore dans l'hypersurface espace-temps. Le choix particulier de coordonnées

qui implique une topologie localement hypersphérique (existence d'une coordonnée radiale r, capable de prendre des valeurs inférieure au rayon de la sphère horizon, de la sphère de Schwarzschild) serait-il pertinent?

Un astrophysicien connu écrivait, il y a quelques années :

- Nous en savons maintenant beaucoup plus sur l'intérieur des trous noirs.

Mais les trous noirs, s'ils existent, ont-ils un intérieur, ou correspondent-ils à une topologie localement hypertorique ?

...On voit tout ce que peut induire un choix de système de coordonnées. La solution géométrique existe. Elle possède des géodésiques. Mais nous ne savons "lire" tout ceci qu'en projetant dans notre espace mental de représentation : un espace temps euclidien, qui n'est même pas relativiste. Choisir un système de coordonnées, c'est choisir un système de lecture, un système de projection.
...Tels les personnages de Platon, nous ne pouvons qu'observer des ombres sur un "écran euclidien". Encore faut-il choisir le bon objectif du "système de projection".

...