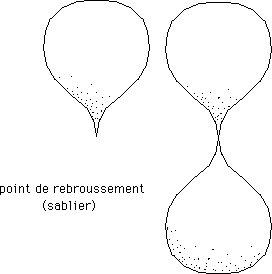
Etc....

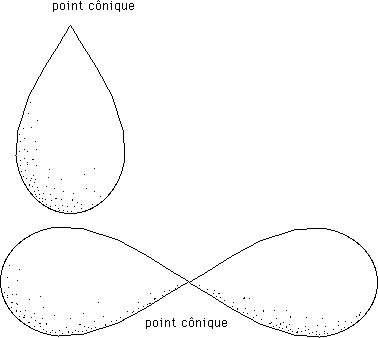
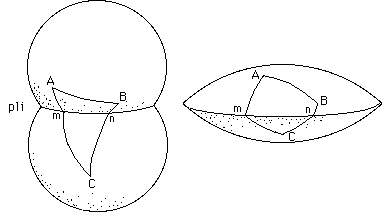
..Au passage le pli est une région particulière de la surface qui contient de la courbure linéique , à gauche négative, à droite, positive. A dessein on a fabriqué ces deux surfaces avec des calottes sphériques. L'objet final a la topologie de la sphère. Il possède donc une courbure totale égale à 4p . Supposons que l'objet de gauche ait été fabriqué avec deux fois trois quarts de sphère (partant de sphères de même rayon). Ces composants correspondent donc chacun à une courbure de 3p. Total 6p . On sait donc immédiatement combien le pli contient de courbure (négative) : - 2p . Celle-ci est uniformément distribuée le long du pli circulaire. On sait donc calculer la somme des angles du triangle ABC. En mesurant sa surface on connaît d'abord la quantité de courbure (angulaire) qu'il contient C'est :

Il faut retrancher la quantité de courbure contenue dans l'arc mn. C'est :

La lentille a aussi la topologie de la sphère. Donc le pli contient une courbure linéique positive égale à 2p.

...On peut également calculer la somme des angles du bizarre triangle ABC, qui est constitué par trois lignes géodésiques. Les géodésiques franchissent allègrement les plis. Vous n'avez qu'à fait l'expérience avec votre ruban adhésif.

L'arc mn contient la courbure linéique : Supposons que l'espèce de lentille indiquée plus hautait été fabriquée avec deux quarts de sphères, identiques. Chacun contient une courbure égale à p . Donc, dans la surface (sans le pli) contient la courbure 2p .

...En comptabilisant la courbure angulaire contenue dans le triangle ABC et dans l'arc-pli on peut connaître l'écart, positif, à la somme euclidienne p .

On voit qu'on peut assez facilement jongler avec ces problèmes de courbure, pour les surfaces.

...Une surface peut comporter des points singuliers ou des plis. Dans ce cas il s'agit de singularités réellement géométriques, intrinsèques, et non résultant d'un choix de coordonnées.

...Au passage notons que cette courbure linéique pourrait être répartie sur une portion de surface. Par exemple, pour la figure de gauche, on obtiendrait :

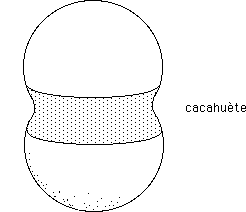
...C'est la démarche analogue à celle qui avait été présentée plus haut, où la courbure concentrée au sommet d'un cône avait été distribuée sur une calotte sphérique (cône émoussé). Si les deux calottes sphériques composant la surface ci-dessus représente par exemple chacune deux tiers de sphère, soit une courbure

La surface grisée contiendra une courbure négative C, uniformément distribuée, telle que :