8

Invariance par changement de coordonnées.

...Voilà un concept-clef de la Relativité Générale, qui n'est pas facile à présenter. Nous avons dit que rechercher une "solution cosmologique", stationnaire ou instationnaire, revient à construire une hypersurface à quatre dimensions qui soit "solution de l'équation de champ".

...Prenons par exemple un objet en tôle qui ait la topologie de la sphère. C'est "une sphère en tôle". Là encore on imagine bien qu'on puisse déformer cette surface en chauffant et en refroidissant par endroits. Par exemple en chauffant en un point et en refroidissant la région antipodale on transformerait cette sphère en œuf. Un œuf est un objet qui a la topologie de la sphère, mais qui est une surface à courbure variable.



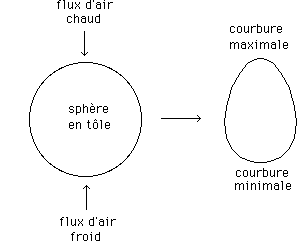
...En chauffant à un endroit et en refroidissant à un autre, on va créer des tensions dans le métal. Bien sûr, comme ce matériau est conducteur, si on cessait de chauffer et de refroidir, la température s'homogénéiserait et l'objet reprendrait sa forme sphérique. Ce qui qui compte c'est qu'on arrive à créer une situation stationnaire avec un champ de température non-uniforme. Ce champ engendre des tensions et on pourrait concrétiser ces tensions sous la forme d'un objet mathématique T appelé tenseur.

Quelque chose décrit la géométrie de l'objet. Cela s'appelle une métrique . C'est à partir de ce second objet mathématique qu'on peut :

- Calculer le tenseur géométrique S

- Calculer les géodésiques de la surface.

La géométrie de cette surface pourrait se calculer à partir d'une équation analogue à l'équation d'Einstein, du style :

S = a T


où a est une constante. En connaissant a priori le champ de température dans la tôle, donc le tenseur des tensions, on pourrait en déduire sa géométrie. La meilleure façon de "lire" cette géométrie serait d'analyser alors le système des géodésiques. Nous connaissons celles de la sphère (ses "grands cercles"). Les géodésiques d'un œuf sont différentes.

...Pour décrire ces géodésiques nous aurons besoin de définir un système de coordonnées sur la surface. Pour la sphère, on pourra prendre le classique système azimut-site.



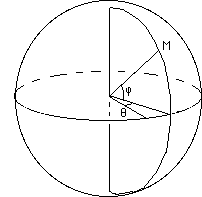
...Dans ce système de coordonnées particulières, les géodésiques de la sphère correspondraient à certaines équations.

Sur cette sphère les courbes q = Cte représentent la famille de géodésiques passant par deux points. Par contre les courbes j = Cte (parallèles) ne sont pas des géodésiques de la surface.

...On pourrait aussi définir un système de coordonnées analogues et écrire les équations des géodésiques de la surface "œuf". Mais on remarque aussitôt une chose essentielle : les géodésiques de la surface sont indépendantes des coordonnées que l'on choisit pour les décrire , de même que les points d'une sphère, ou d'un œuf, existent, indépendamment du système de coordonnées utilisé pour les repérer.

...De même, sur un plan, on peut représenter des points en coordonnées cartésiennes ou en coordonnées polaires. Les droites du plan sont des géodésiques.

Une droite peut être décrite dans deux systèmes de coordonnées :



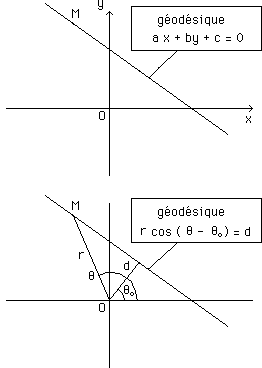
...Il s'agit de la même géodésique, avec deux descriptions totalement différentes. Les droites du plan existent indépendamment de la manière dont on les décrit, du choix des coordonnées utilisées. Et on peut en imaginer... une infinité.

...Alors, qu'est-ce qui est intrinsèque ? Réponse : la longueur s mesurée sur une droite (ou le long d'un contour curviligne quelconque). Entre deux points M₁ et M₂ d'une surface le trajet de longueur minimal est une géodésique.

...De même la distance séparant deux points, sur une géodésique des objets "sphère" ou "œuf" est également une grandeur qui est indépendante du système de coordonnées choisies. Si on prend deux points M₁ et M₂ sur une surface et qu'on trace l'arc géodésique qui les joint, la longueur s mesurée le long de cet arc sera la même, quel que soit le système des coordonnées utilisé pour repérer les points.



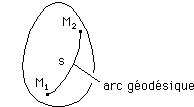
...Il en est de même pour l'hypersurface à quatre dimensions que nous appelons "univers". Elle possède son système de géodésiques, également invariantes par changement de coordonnées. Nous n'habitons pas dans un espace (x , y , z , t) avec des coordonnées de position et une coordonnée de temps, mais dans une hypersurface quadridimensionnelle qui peut être entièrement décrite par son réseau de géodésiques. Sur ces géodésiques il existe une longueur s qui est également invariante par changement de coordonnées. Les points de cette hypersurface ne sont plus des points de l'espace, mais des points d'une hypersurface espace-temps. On les appelle des événements . Deux événements distincts sont donc séparés par quelque chose qu'on appelle s. Mais qu'est-ce que c'est donc ?

C'est le temps propre .

...Une trajectoire géodésique dans cette hypersurface espace-temps sépare deux événements M1 et M2. Tout ce que je puis dire c'est que si j'avais utilisé un véhicule pour effectuer ce trajet dans l'espace temps, il se serait écoulé un laps de temps s, sur mon horloge de bord.

  Un choix de coordonnées consiste à repérer les points de l'espace temps par des coordonnées d'espace (x , y , z) et une coordonnée de temps t . Mais comme ce choix est arbitraire cet espace et ce temps n'ont pas d'existence intrinsèque. Ce ne sont que des façons de "lire" la surface, de la parcourir. Seule contrainte : en fonction de l'hypothèse faite, on ne peut se déplacer que selon des géodésiques et sur ces dernières, la seule chose fiable à laquelle on peut s'accrocher, c'est le "temps propre écoulé" s, et non ce temps t , simple système de repérage chronologique (chronological marker).

Pour chaque choix du système de coordonnées, un système différent de lecture des événements, des phénomènes.

...Les physiciens ont donc cherché un formalisme qui soit indépendant du choix des coordonnées. C'est l'essence du formalisme tensoriel . On ne peut pas en dire plus sur ce sujet, sous peine d'entrer dans des détails techniques relativement complexes.

 
Le problème des singularités.

Sur une sphère, le choix de coordonnées angulaires classique introduit deux singularités polaires.



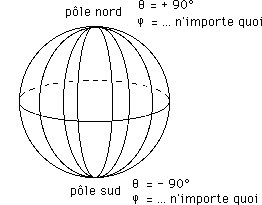
Impossible de cartographier une sphère sans introduire ce genre de singularités polaires.

...A noter qu'on peut cartographier une sphère avec une singularité unique. On crée sur la sphère une première famille de courbes (des cercles) en la coupant par des plans, comme indiqué ci-après :



Puis une seconde famille :



En dehors de cette unique singularité, pas de problème. Si on regardait cette sphère de l'autre côté, on verrait ceci :



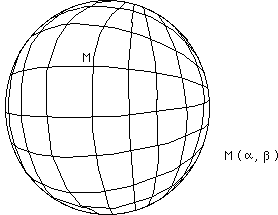
...En dehors de l'unique singularité S, on repère les points sans difficultés. Mais les valeurs des paramètres a et b définissant cette singularité de maillage S sont .... n'importe quoi...

...Pourtant une sphère n'est pas géométriquement, intrinsèquement singulière. Tournez une boule de billard en tous sens, ou un œuf, vous n'y découvrirez aucun point singulier.

Ces singularités-la ont donc été créées par le choix des coordonnées.

   

   Sommaire article      Sommaire Science       Page d'Accueil

Retour vers Guide-Sciences

Nombre de consultations de cette page depuis le 1° juillet 2004 :