Géométries conjuguées.

...Nous allons associer alors un posicône émoussé et un "négacône émoussé", comportant les mêmes quantités de courbure, mais de signe opposé : + q et - q. On peut les mettre face à face (en créant au passage une "application point par point" : bi-univoque, injective ). Il y a alors deux nappes. Appelons-les F et F*. A tout point de F correspond un point de F*.

...Débrouillons-nous pour que les contours circulaires des "parties émoussées", porteuses de courbure (positive dans une nappe, négative dans l'autre) se correspondent point par point. On illustre ceci en projetant le tout sur un plan. On obtient deux surfaces ayant des courbures conjuguées.

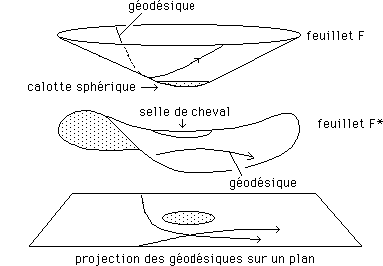
...Les flanc côniques sont "non-courbes", ce sont des éléments de surfaces euclidiens. On dira qu'en tout point de ces surfaces la courbure locale est nulle. La calotte sphérique et la selle de cheval se correspondent point par point. Leurs courbures sont opposées.
 

La Relativité Générale.

...Le point de départ est l'idée que la géométrie du cosmos est déterminée par son contenu en "énergie-matière". Notons qu'on emploie le vocable énergie-matière et non seulement matière, ce qui montre bien que tout contenu cosmique a une influence sur la géométrie, y compris le rayonnement, les photons (ou les neutrinos). Nous avons vu plus haut qu'un photon créait une mini-courbure positive dans l'espace.

...Nous allons d'abord raisonner en stationnaire. Une surface plane, libre, est une surface où la tension est nulle. On peut modifier sa géométrie en y créant des tensions, positives ou négatives (le signe est une question de conventions). Si je chauffe par exemple un film plastique je pourrai y faire apparaître une cloque, c'est à dire une région à courbure positive.

...Je peux aussi mettre à la surface d'une feuille de papier un produit qui, en sèchant, va se contracter. La tension fera apparaître une région à courbure négative.

...Un chaudronnier formeur sait jouer sur ces tensions pour déformer une tôle. Prenons par exemple un tube de métal. Je chauffe d'un côté, je refroidit de l'autre. Que va-t-il se passer ?

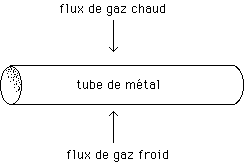
Le tube va se courber, la partie chauffée se dilatant et la partie refroidie se contractant.

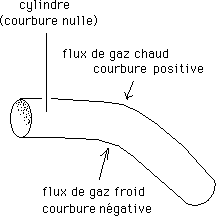
...Ce faisant, nous avons créé des tensions dans le métal. C'est l'origine du mot tenseur, en mathématiques et en géométrie. Le spécialiste de résistance de matériaux parlera de tenseur des contraintes . Le géomètre parlera de tenseur de courbure .

La petite expérience ci-dessus illustre l'idée :

...En Relativité Générale, on fait de même. La différence est que ce contenu local en énergie-matière détermine la géométrie d'une hypersurface à quatre dimensions et non, comme ici, la géométrie d'une surface à deux dimensions. Mais l'idée est similaire.

...Le mathématicien utilisera alors une écriture tensorielle . On ne peut guère en dire plus ici pour un non-mathématicien. Mais le tenseur d'Einstein S (on utilisera des lettres grasses) correspond à l'aspect géométrie. Dans l'équation d'Einstein on l'identifie à un autre tenseur T, qui décrit le contenu en énergie-matière, à une constante multiplicative près, la "constante d'Einstein c ".

La célèbre équation d'Einstein s'écrit donc :

...Dans le tenseur T interviennent la masse volumique r et la pression p (en fait le tenseur T le plus général est plus complexe, mais nous nous contenterons de cette expression, usuelle, d'ailleurs). Dans une configuration stationnaire on se donnera donc une certaine distribution de densité et de pression r (x,y,z) , p (x,y,z). Avec ceci on sait construire le tenseur T qui contient ainsi toutes les données du problème. La question est alors : "quelle est la géométrie qui va avec ce tenseur T , satisfaisant l'équation ci-dessus ? ".

...Autrement dit, le physicien, connaissant le contenu local de l'univers cherche à déterminer la géométrie de l'hypersurface univers.

Qui dit géométrie dit géodésiques. C'est ici qu'intervient la deuxième hypothèse de la Relativité Générale :

A ce stade, une remarque : où sont les particules dans toute cette affaire-là ?

...Réponse : le spécialiste de la Relativité Générale fait dans le macroscopique. Les fonctions-entrées du problème, la masse volumique r et la pression p, correspondent à une description macroscopique du contenu cosmique. Même chose pour la "sortie". Et le géomètre d'ajouter :

- Vous m'avez donné des fonctions r (x,y,z) et p (x,y,z), je vous ai construit l'hypersurface qui allait avec, avec ses familles de géodésiques. Mais je ne peux pas faire plus. Je suis en particulier incapable de vous fabriquer des particules, des atomes, etc. Pour cela, voyez un autre service...

En clair : le pont entre la Relativité Générale et la physique des particules n'est pas encore bâti.

Mais l'astronome s'écrira :

- Qu'importe. Cette hypothèse selon laquelle les photons suivent certaines géodésiques de cette hypersurface fonctionne. La preuve : je peux faire des observations. Si je suppose que les planètes, assimilées à des masses ponctuelles, suivent également des géodésiques de cette hypersurface, je peux construire leurs trajectoires. Il y a aussi les effets de lentille gravitationnelle....

Il a raison.

...Ces effets de lentille gravitationnelle, disons-en quelques mots. Bien sûr, cette image du cône émoussé n'est qu'une image didactique. Une planète qui orbite circulairement autour d'une étoile suit aussi une géodésique de l'espace temps. Or un cercle tracé sur une cône émoussé n'est pas une géodésique :

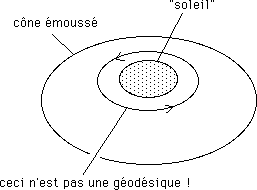
Cela montre simplement les limites des images didactiques, fussent-elles géométriques.

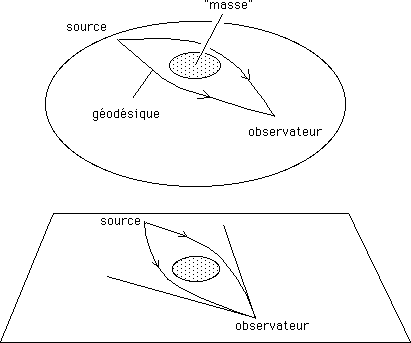
...Les photons suivent effectivement des géodésiques de l'hypersurface espace-temps. On pourra se servir de cette image du cône émoussé pour l'illustrer. Les rayons lumineux peuvent passer de part et d'autre d'un objet massif, puis converger vers l'observateur. Si nous projetons ces géodésiques, nous obtiendrons un effet de mirage : l'observateur aura l'impression qu'il y a deux sources au lieu d'une :

   Sommaire article      Sommaire Science       Page d'Accueil

Retour vers Guide-Sciences

Nombre de consultations de cette page depuis le 1° juillet 2004 :