...Nous pouvons fabriquer une sphère en juxtaposant des mini posicônes. Mais lors de cette opération, cette surface à courbure (ou densité de courbure ou courbure locale) constante, va se refermer. Elle contient donc une certaine courbure, mais laquelle ?

...Si je trace un triangle géodésique sur une sphère, il va enserrer un certain nombre de mini posicônes, une certaine "quantité de courbure", qui est un angle. Celle-ci sera simplement proportionnelle à la surface du triangle, ou plus précisément au rapport entre la surface s du triangle et la surface S de la sphère.

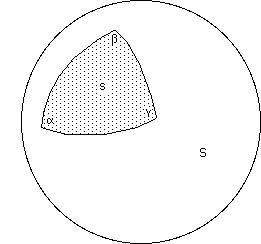
...Mais nous avons vu, plus haut, que lorsque nous tracions un triangle géodésique sur une surface fabriquée à partir de posicônes joints, l'écart à la somme euclidienne était égal à la somme des courbures concentrées liées à chaque sommet de cônes contenus dans notre triangle. Il suffit donc de mesurer la somme des angles a , b , g du triangle ci-dessus, fabriqué à partir de trois arcs géodésiques de sphère pour obtenir une mesure de la quantité de courbure angulaire contenue dans ce triangle.Les géodésiques de la sphère sont ses "grands cercles".

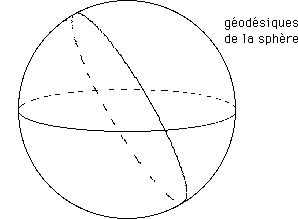
...Coupons notre sphère en huit portions égales. Nous obtiendrons huit triangles constitués par des arcs géodésiques, dont les trois angles seront droits.

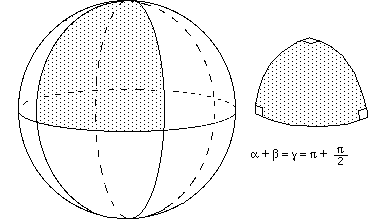
...Chacun de ces triangles contient donc une courbure égale à p/2 . Comme il y en a huit, la courbure totale de la sphère vaut donc 4 p.

...Cette petite remarque pour montrer qu'on peut construire des résultats géométriques à l'aide de raisonnements extrêmement simples.

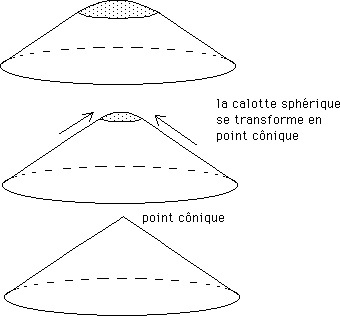
...Revenant au thème du cône émoussé, on voit que le flanc de l'objet dépend de la quantité de courbure "contenue à l'intérieur", cette courbure pouvant être ponctuelle (point cônique) ou distribuée sur une calotte sphérique. On peut faire tendre la calotte vers un point, en la réduisant de manière homothétique (de telle manière qu'elle contienne toujours la même "quantité de courbure").

Trajectoires.

 ...En Relativité Générale l'idée clef est simple : assimiler les trajectoires des objets, des particules, des photons ou de la matière à des géodésiques. Bien sûr, ce sont des géodésiques d'une hypersurface à quatre dimension. Donc nous n'avons là aussi que des images didactiques.

Si on prend notre cône émoussé on peut tracer dessus des géodésiques, et les projeter sur un plan.

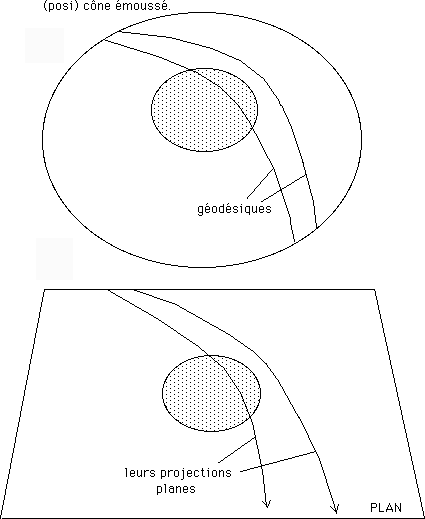
...Toutes les particules suivent des géodésiques de l'hypersurface : les particules de matière, mais aussi le photons et les neutrinos. C'est pour cela que nous nous sommes amusés à figurer une géodésique qui traverse l'objet complètement. Un neutrino peut traverser le soleil sans problème.

...Mais qu'est-ce que ce plan sur lequel on projette ces géodésiques ? C'est la manière dont nous représentons l'espace. Notre "univers mental" est complètement euclidien et notre pensée "plate". Quand nous voyons une comète frôler le soleil, il ne nous viendrait jamais à l'idée qu'en fait elle va "tout droit", c'est à dire qu'elle suit une géodésique de l'hypersurface. Notre perception du monde, c'est la figure 24' , où un astre "attire" les objets qui passent dans son voisinage.