...Lorsque nous avions tracé notre triangle, constitué par des lignes géodésiques, sur un plan, la somme de ses angles au sommet valait p. Un plan... est une surface plane, "non courbe", euclidienne. La somme des angles de ce triangle est donc la somme euclidienne. Dans l'expérience précédente nous avons vu que si un triangle ne contenait pas le sommet de notre cône, la somme restait euclidienne. Par contre quand le triangle contient le sommet S, alors cette somme présente un excès q, quel que soit le triangle, du moment qu'il contient ce point. Nous dirons que le sommet du cône est un point de courbure concentrée.

...Nous pouvons maintenant passer à d'autres expériences. Après avoir fabriqué deux cônes, avec des découpes q1 et q2 nous pouvons coller ces deux éléments de surface l'un à l'autre.

...Une façon plus simple de procéder consiste à opérer deux découpes dans une feuille de bristol et à fabriquer la surface suivante :

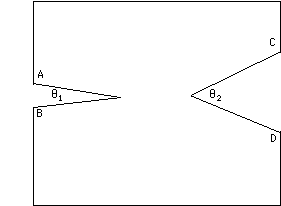
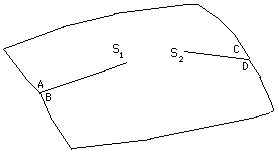
Vous pourrez alors tracer sur cette surface autant de triangles géodésiques que vous voudrez :

- N'enserrant ni S₁ ni S₂ : Somme des angles : p

- Enserrant seulement S₁ : Somme des angles p + q₁

- Enserrant seulement S₂ : Somme des angles : p + q₂

- Enserrant les deux points S₁ et S₂ : Somme des angles : p + q₁+ q₂

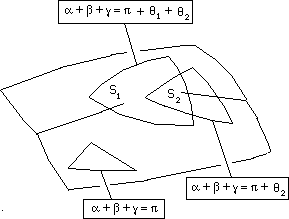
...On imagine aisément qu'on puisse fabriquer un grand nombre de mini posicônes d'angle Dq faible et qu'on puisse les coller les uns sur les autres. On pourrait même se débrouiller pour qu'il y ait une densité de courbure constante par unité de surface, en assimilant cette courbure à la somme des Dq associés à chaque sommet de ces mini posicônes.

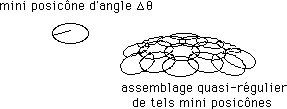
...En rendant ces mini posicônes de plus en plus petits (de même que l'angle élémentaire Dq qui leur est associé) on peut se servir de ceci pour construire une portion de surface à densité de courbure constante.

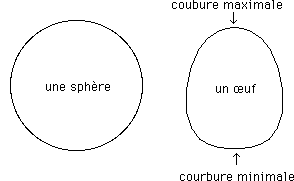
La sphère est une surface à densité de courbure constante. On dira plus simplement à courbure locale constante.

Un œuf est une surface courbe, à densité de courbure variable. On dira plus simplement à courbure locale variable.

...La Relativité Générale consiste à identifier masse volumique r et courbure locale. Bien sûr, la relativité Générale traite non pas de surfaces à deux dimensions, ni même à trois, mais d'hypersurfaces à quatre dimensions. Il ne faut donc pas trop demander à ce qui précède et nous ne devrons considérer ces figures que comme des images didactiques, destinées à fixer les idées. Mais elles ne sont pas si mauvaise que cela.

 
Image didactique 2d d'un astre.

 Un astre, comme le soleil, est une concentration de matière, entourée,sinon de vide, du moins d'un quasi-vide (donc d'une région à courbure très faible). En deux dimensions l'image didactique sera celle d'un cône émoussé.

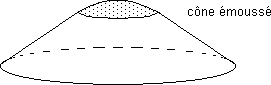
...Un cône émoussé est fabriqué à l'aide de deux éléments : une calotte sphérique, à courbure constante (ou à "densité de courbure constante") et un tronc de cône. Ce tronc de cône est "plat", sa densité de courbure est nulle. C'est une surface euclidienne. C'est l'image didactique 2d d'un astre de masse volumique r constante.

...On pourrait au passage se demander comment raccorder parfaitement un tronc de cône et une calotte sphérique, de manière à ce que le plan tangent soit continu.

...C'est simple. Le tronc de cône est fabriqué à partir d'un cône, lequel implique une découpe d'un angle q . La calotte sphérique contient une certaine "quantité de courbure", qui est aussi un angle. C'est la somme de tous les angles des mini posicônes qui la constituent. Il faut que ces deux angles soient égaux.

Mais comment évaluer la quantité de courbure contenue dans une calotte sphérique donnée ? .

...

 Sommaire article      Sommaire Science       Page d'Accueil

Retour vers Guide-Sciences

Nombre de consultations de cette page depuis le 1° juillet 2004 :