 |
2
|
 |
2
|
...Dans tout ce qui va suivre nous ne traiterons que de surfaces à deux dimensions. Il serait préférable que le lecteur se munisse d'un peu de matériel avant d'entamer cette lecture. Il y a en effet des choses qui "se comprennent avec les mains", en effectuant des expériences. Il faut donc:
- Des feuilles de papier bristol, ou de papier un peu fort.
- Un ruban adhésif, si possible coloré.
- Des ciseaux.
...On trouve dans le commerce des rubans en "scotch toilé" particulièrement commodes, qui ont l'avantage de pouvoir être déroulés en bandes de largeurs quelconques.
...Prenez une surface, par exemple la carrosserie de votre voiture. Vous pouvez coller une bande sur celle-ci, en vous arrangeant pour que celle-ci ne plisse pas, qu'elle adhère toujours complètement à son support. Ce faisant vous tracerez des géodésiques de la "surface-voiture".
...Si vous faites cette opération sur une surface plane, vous obtiendrez.. des droites. Les droites sont les géodésiques du plan.
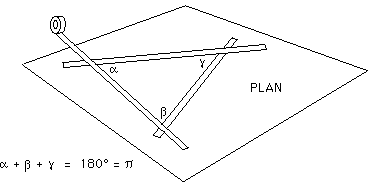
...Avec trois géodésiques vous pourrez tracer un triangle sur ce plan, "surface euclidienne", la somme des angles de ce plan valant 180°.
Les posicônes.
Fabriquons maintenant un "posicône". Pour ce faire, effectuer une découpe d'un angle q et recoller la surface comme indiqué.
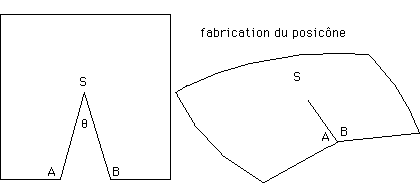
...Traçons deux triangles géodésiques, avec le ruban adhésif, l'un étant extérieur au sommet S de ce posicône et l'autre contenant ce sommet S. Mesurons la somme des angles du triangle. On constate alors que la somme des angles du triangle qui ne contient pas le sommet reste égale à 180° alors que celle de l'autre triangle vaut 180°+q .
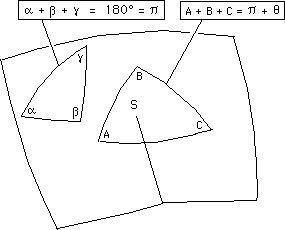
Pour le vérifier il suffirait de rouvrir ce "posicône" et de le mettre à plat. Alors on obtiendrait ceci :
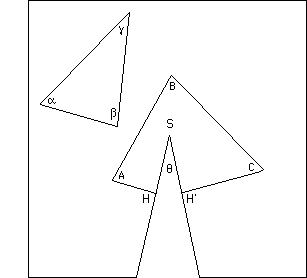
...On peut alors vérifier aisément que les droites AH et H'B font un angle q. Comme on pourrait le constater "expérimentalement", les géodésiques du cône, après mise à plat, deviennent des droites du plan, ce qui signifie simplement que le cône est une surface développable. Même chose pour un cylindre.
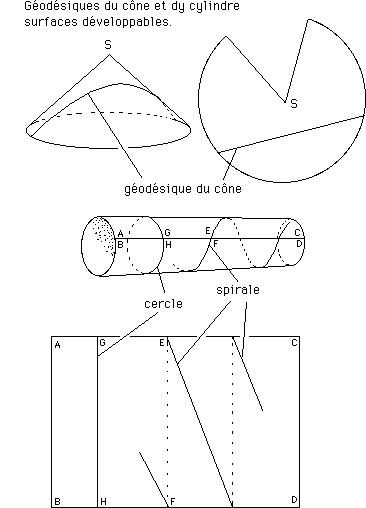
...Une surface développable est également une surface qu'on peut rouler sur un plan (modulo certaines précautions, pour les surfaces développables à courbure négative, comme on le verra plus loin).
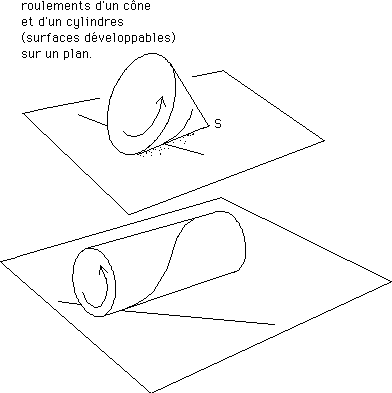
...Si on trace une géodésique
sur un cône ou un cylindre, avec de l'encre grasse, on peut se servir
de cette "matrice" pour "l'imprimer" sur un plan, auquel cas on obtient une
droite. Et, inversement, si on inscrit une droite à l'encre grasse
sur un plan et qu'on "l'imprime" sur un cône ou un cylindre, en faisant
rouler ces objets sur le plan, l'impression donne des... géodésiques.
Sommaire article Sommaire Science Page d'Accueil
Retour vers
Guide-Science
.
Nombre de consultations de cette page depuis le 1° juillet 2004
: