Projet Epistémotron

1

Généralités sur le problème à N corps
Quelques notions de théorie cinétique des gaz

L'astrophysique est en principe une science qui se donne pour but de comprendre les phénomènes qui sont à l'oeuvre dans le cosmos, à différentes échelles. Il y a par exemple la façon dont s'est formé le système solaire, qui est en soi un travail tout à fait passionnant, qui n'a jamais été fait. Ca sera un des buts poursuivis dans le projet Epistémotron et ces travaux concrétiseront la théorie élaborée par le mathématicien Jean-Marie Souriau.

A une échelle plus grande on trouve la dynamique galactique, totalement opaque jusqu'à ce jour. Nous n'avons aucun modèle de galaxie. Nous ne savons pas comment ces objets se forment ni comment ils évolue. Au plan purement théorique ces "systèmes à N corps, auto-gravitants" se gèrent à travers un système d'équations différentielles (Vlasov plus Poisson). Jusqu'à présent ces approches (que les actuels "théoriciens" ne connaissent même plus, du reste) se sont également heurtées à des murs.

La solution nous semble passer par une nouvelle vision du cosmos, gémellaire. Le lecteur intéressé trouvera une initiation à ce thème dans un dossier présent sur mon site depuis de longues années. Concrètement ceci revient à envisager que l'univers ait deux composants :

- Des particules à énergie positive, les nôtres

- Des particules à énergie négative, gémellaires.

Comme E = m c² les particules à énergie négative se comportent comme si elles possédaient une masse négative. On obtiendra donc le schéma dynamique suivant :

- Deux masses positives s'attirent selon la loi de Newton

- Deux masses négatives s'attirent selon la loi de Newton

- Deux masses de signes opposés se repoussent selon "anti-Newton".

Pourquoi n'observons-nous pas optiquement les particules à énergie négative ? Parce que l'interaction entre deux particules d'énergies opposées, via l'interaction électromagnétique est tout simplement impossible. Comme montré récemment par un jeune et brillant chercher ces deux particules, selon la théorie quantique des champs, si elles interagissent de cette façon doivent échanger des "particules virtuelles" ou "carriers", qui sont des photons à énergie positive et des photons à énergie négative. C'est la prise en charge de toutes les interactions possibles à travers l'intégrale des chemins de Feynman conduit dans ce cas à un résultat .. nul. L'interaction est donc simplement impossible et les particules gémellaires restent pour nous invisibles. Elles peuvent nous traverser également sans interagir autrement qu'à travers la gravitation (ou plutôt l'antigravitation). Cette idée est la clé de tous les grands problèmes du moment en astrophysique et en cosmologie ( effet de masse manquante, courtes de rotation des galaxies, formation des galaxies, origine de la structure à grande échelle de l'univers). Le lecteur trouvera une présentation vulgarisée de ces idées dans mon ouvrage paru en 1997 :

Des informations générale, se référant entre autre à l'instabilité gravitationnelle pourront être trouvées dans ma bande dessinée " Mille Milliards de Soleils ", présente sur le CD-Rom "Lanturlu1" sous format pdf, imprimable (on peut acquérir les 18 bandes dessinées en envoyant 16 euros à J.P.PETIT, chez Jacques Legalland, Lou Garagai, 13770 Venelles.

Différents mécanismes sont à l'oeuvre dans le cosmos en dehors de la gravitation. Mais dans tout ce qui suivra on se focalisera sur ce mécanisme unique en négligeant les échanges radiatifs et la production d'énergie par fusion. Les systèmes que nous étudierons seront des "systèmes à N corps", auto-gravitants, baignant dans leur propre champ de gravité. On voit que pour étudier le comportement d'un tel système il faut, pas après pas, étudier le déplacement de chaque "point-masse" (de masse positive ou négative) en effectuant la somme vectorielle de toutes les forces gravitationnelles, d'attraction de répulsion issues des N-1 autres particules. Le temps de calcul croîtra donc, de manière brute selon N(N-1) ou N² su N est grand, ce qui sera toujours le cas.

Dans un système planétaire ou proto-planétaire le nombre d'objets est relativement faible et peut être géré par un unique ordinateur "domestique". Ca n'est pas le cas pour une galaxie. La nôtre est composée par cent à deux cent milliards d'étoiles, assimilables à des points-masses. Ce masse d'étoiles est alors assimilable à un gaz, dont les molécules seraient les étoiles elles-mêmes, assimilables à de simples points-masses. Pour se rapproche au maximum "de la réalité" on devra donc envisager de gérer le plus grand nombre de points-masses possible. Ces techniques ont été mises en oeuvre dès la fin des années soixante. Forte heureusement la rapidité des ordinateurs et leur puissance de calcul n'a fait que croître au fil des années. J'ai pu ainsi faire effectuer des calculs au début des années quatre vingt dix sur le gros ordinateur qui, au centre allemand DAISY (accélérateur de particules) gérait les données des expériences. A cette époque une telle machine, considérée comme exceptionnellement puissante, pouvait gérer 5000 points-masses. Le lecteur trouvera dans l'ouvrage ci-dessus les résultats essentiels trouvés lors de cette expérimentation numérique.

Il se trouve que l'informatique a fait de tels progrès en douze ans que ces problèmes peuvent maintenant être traités sur des machines "domestiques" du fait de l'accroissement considérable de leur vitesse de calcul (horloge en 2 gigahertz) et de leur mémoire centrale. Des lecteur comme Olivier le Roy on donc pu retrouver quelques aspects essentiels, simples, comme le mécanisme de l'instabilité gravitationnelle en programmant en C++ leur propre machine. Alors que, de guerre lasse, j'avais totalement abandonné l'astrophysique en 2001 cet initiatives individuelles m'ont incité à essayer de relancer une recherche fondée sur les actions ... d'amateurs. En effet, depuis douze ans, comme le notait l'Académicien et Astrophysicien Jean-Claude Pecker à l'issue de la conférence que j'ai donnée le 25 février au Collège de France il est étonnant et regrettable que des équipes dotés de moyens ad hoc n'aient pas repris cette idée, continuant à bricoler assez lamentablement avec "de la matière sombre froide".

Je me sens donc tenu de fournir à tous ces gens "qui veulent en découdre" tous les éléments nécessaires pour qu'ils puissent avancer dans cette démarche. De nombreux calculs sont possible avec une seule machine et un nombre de points inférieur à 2000-5000. Ceci limite le travail à des simulations bidimensionnelles. On ne saurait, en 3d, considérer un ensemble de quelques milliers de points comme un "gaz". Au-delà, un projet fantastique se dessine : faire collaborer N machines en mettant en oeuvre une technique de "calcul partagé". C'est alors un délicat problème de développement, de la pure informatique.

Gestion d'un problème à N corps.

Nous avons des points-masses et des conditions initiales qui se résumerons à six nombres en 3d (trois coordonnées de position et trois composantes de la vitesse) et à quatre en deux dimensions (deux coordonnées de position et deux composantes pour la vitesse). Il nous faut aussi nous situer dans un espace de calcul et gérer des conditions aux limites (un ordinateur ne sait pas gérer un espace ... infini). Il nous faut ensuite régler au mieux l'intervalle de calcul, le pas temporel Dt. Commençons par une vision très schématique. Imaginons un espace de calcul 2d, infini. Ce que les mathématiciens appellent R2. Dans cet espace nous plaçons N points avec des positions et des vitesses initiales. Prenons une des particules (marquée en noir) et calculons la résultantes ( F_x, F_y , F_z ) des forces exercées sur elle par les N-1 autres particules. On calculera ensuite la nouvelle position et la nouvelle vitesse de cette particule à l'aide d'un développement de Taylor.

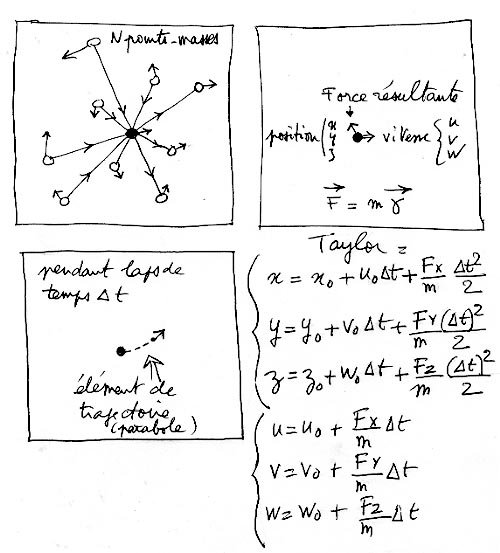
Un problème se pose immédiatement à nous : comment choisir l'intervalle de temps Dt ? Le raisonnement est simple. Nous ne pouvons pas gérer simultanément les déplacements des N particules. Nous sommes obligés de "geler" le champ gravitationnel pendant ce temps Dt. Effectuons un pas de calcul et traçons les trajectoires des particules dans ce champ "gelé" en utilisant le développement de Taylor ci-dessus. Leur mouvement va modifier in fine la distribution locale du champ. Le calcul sera valable si le champ "n'est pas trop modifié". A l'oeil la distribution des masses n'aura "pas trop varié" pendant ce temps Dt. Donnons une image 2d. Imaginez que vous placiez des billes de plomb sur un matelas en mousse. Celles-ci vont en déformer la surface. Une accumulation de billes créera, localement, une cuvette. Nous avons une représentation matérielle du champ de gravitation sous la forme d'une surface. C'est aussi une bonne image didactique d'un système "auto-gravitant" car les billes se déplacent sur une surface qu'elles modèlent elles-mêmes.

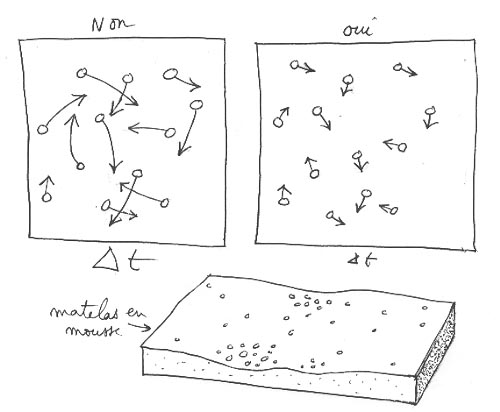
L'analogue du calcul consistera à créer une autre "carte" en calculant le déplacement de toutes les billes sur ce matelas mousse supposé gelé, rigide. On obtient une autre distribution des billes, que l'ont va alors plaquer sur un matelas en mousse identique au premier. Il va alors se creuser. On considérera que le pas de calcul est acceptablement faible si, globalement, les surfaces sont voisines.

On notera qu'on appliquerait le même critère si on considérait un ensemble de 5 étoiles formant un mini-amas, en étant liées par la gravitation. A l'instant t elle créent un champ de gravitation g (r,t). On peut calculer le déplacement de chacune d'entre elles pendant un temps et recalculer ce même champ g' (r + Dt). Le calcul sera valable si pendant cet intervalle de temps les deux champs et sont "suffisamment voisins".

Bien sûr, plus le pas sera faible et plus rapide sera le calcul, mais plus grande sera l'erreur. Dans ce qui va suivre nous nous intéresserons à l'évolution de systèmes où N sera grand et même le plus grand possible. Au minimum plusieurs milliers de points-masses Quand il sera possible de travailler en "calcul partagé" : plusieurs millions de points-masses (ce qui nous ouvrira les portes d'un 3d valable). On voit tout de suite ce qui est visé : réussir à gérer cet ensemble d epoints-masses comme un gaz de particules. Cette idée nous parait intuitive s'ils s'agit d'une masse de gaz interstellaire. Mais il sera de même pour l'ensemble des étoiles constituant une galaxies. La nôtre en contient entre cent et deux cent milliards. Dix fois plus pour une galaxie elliptique. A l'échelle de notre perception proche notre galaxie nous parait très raréfiée. Les distances des étoiles les plus proches se situent en années-lumière. Mais il s'agit d'une distance bien faible à l'échelle de la galaxie elle-même, dont le diamètre est de quelque cent mille années lumière. Cent années lumière représentent le millième du diamètre d'une galaxie. Or un tel volume contient un nombre important d'étoiles. A l'échelle de la centaine d'années lumière une galaxie se présente comme une masse gazeuse. Jadis, quand on ne disposait que d'outils mathématiques, on tentait de décrire ces objets avec des fonctions continues.

Pour le moment nous avons un espace de calcul ... illimité. Imaginons, pour fixer les idées que nous soyons en 2d. Vous allez pouvoir visualiser l'état du système sur votre écran. Si vous voulez avoir simultanément les informations en position-vitesse vous pourriez par exemple représente les points masses par des taches noire en les associant à un petit trait, un petit segment figurant leur vecteur vitesse. Bien que vous traitiez ces objets comme des masses ponctuelles, rien ne vous empêche de décider de mettre des points plus ou moins gros, selon les masses. Pour être plus près de la réalité vous pourriez décider de faire figurer des petits confettis noirs dont le rayon croîtrait comme la racine cubique de la masse.

Quid d'un système à deux corps ? A priori c'est un système stable. Je crois qu'il faut créer soi-même ses propres programmes pour manipuler soi-même les phénomènes, les avoir sous les yeux. Si vous prenez deux masses M et m très dissemblables, vous aurez l'équivalent d'une planète orbitant autour d'une étoile. Je vous rappelle que le rapport entre la masse du Soleil ( 2 10³⁰ kilos) et celle de la Terre ( 6 10²⁴ kilos) il y a un facteur 333.333 , trois cent mille. Comme Jupiter est 317 fois plus massif que la terre, le rapport masse du Soleil sur masse de Jupiter est de l'ordre de 1000.

Je vous conseille au passage d'acheter le Dictionnaire de l'Astronomie, chez Larousse, où vous pourrez trouver des tas de valeurs d'à peu près n'importe quoi.

Si vous partez d'un problème à 2 corps avec un "Soleil" et un "Jupiter" vous obtiendrez quasiment les lois de Kepler, si vous placez l'étoile à distance suffisante (orbite de Jupiter voisine de 800.000.000 km). On raisonne en astronomie en termes d'UA, d'unités astronomiques. Une UA est la distance moyenne Terre Soleil, soit 150 millions de km. Le rayon de l'orbite jovienne est donc de 5,2 UA.

Dans ces conditions l'étoile sera pratiquement immobile alors que quand on a un système à 2 corps ils orbitent tous les deux autour de leur centre de gravité commun. Parmi les exercices à faire : changer de rapport de masses, rapproche la planète de l'étoile. Regarder comment tout cela fonctionne, avec toujours en arrière plan le choix d'un pas de calcul "suffisamment faible" pour que le résultat soit "significatif". Il existe bien évidemment des programmes tous faits qui vous donnent des choses de ce genre, et cela depuis des décennies. Mais l'intérêt est de créer des choses "où on puisse envoyer les mains". On passe alors à un système à trois corps et là, son comportement change radicalement. Ces systèmes sont instables. A moins de placer deux mini-planètes en orbite autour d'une étoiles, si les masses sont voisines, les objets virevoltent et, tôt ou tard un des membres du trio se trouve éjecté. Vous pouvez retrouver cela assez aisément en réglant vos paramètres. Vous pouvez visualiser les trajectoires et les vecteurs-vitesse, réaliser des gif animés. Il est certain que si quelqu'un faisait cela je serai ravis d'illustrer ce cours avec son travail, en le citant. Je pourrais programmer tout cela moi-même. Hélas, les ordinateurs ont beaucoup change, par rapport au temps où je créais des programmes de conception assistée par ordinateur déjà assez raffinés. Mais de nos jours, si on ne jongle pas avec le C ++ on n'est plus qu'un vieux crabe. Pour tout vous avouer j'ai toujours tout écrit en BASIC compilé. Je ne connais même pas le Pascal ! Il faudrait que je m'y mette. Mais en ce moment nous avons deux bateaux en chantier, deux maquettes, destinées à être télécommandées (si quelqu'un veut participer activement, pas de problème...). L'une est un bateau péruvien d'il y a 5000 ans, une espèce de radeau du Kon-Tiki avec "garas" avec dérives et l'autre un essai de représentation de bateau égyptien de l'Ancien Empire ( 2300 av JC). Donc faute d'avoir le temps d'apprendre le Pascal je compterai sur mes lecteurs pour me fournir les illustrations de ce cours, éventuellement animées.

Les systèmes à plus de deux corps sont instables. La preuve qu'il en est ainsi est que les étoiles que vous voyez dans le ciel sont par moitié des étoiles célibataires, par moitié (grosso-modo) des systèmes doubles ou à plus de deux étoiles. Seuls les deux premiers sont stables. Selon ce qu'on croît savoir les étoiles ne naissent pas isolément mais dans des amas. Paradoxalement cela reste une idée assez récente. Je me rappelle la remarque que m'avait fait mon ami Pierre Guérin, décédé, il y a 15 ou 20 ans :

- Si tu dis que le Soleil est né dans un amas, tu vas de faire mal voir des astrophysiciens.

Depuis un papier de Serge Jodra, paru il y a quelques années dans Ciel et Espace, intitulé "où sont passées les soeur du Soleil" on est passé à l'idée inverse. Bien sûr, il ne s'agit que de spéculations, et un des buts que nous poursuivrons sera, entre autre, d'essayer d'apporter un peu plus de clarté dans ces questions... nébuleuses. Bref on suppose qu'une étoile comme le Soleil serait née dans un amas de quelques centaines d'étoiles. Il n'y a aucune raison a priori pour que ces étoiles aient toutes les mêmes masses. Il se trouve, et ça c'est l'observation qui nous le dit, que le soleil représente en quelque sorte "l'étoile standard" de notre galaxie, et des autres, probablement. Il y a des plus massives et des plus légères. Cela peut donc être intéressant (en passant quand même au 3d) d'étudier le comportement de 200 points-masses interagissant les uns avec les autres. Ces objets représentent une masse totale M. A partir d'une masse M on peut toujours calculer une vitesse de libération. Soit R le rayon de cet "essaim" (il s'agit de cibler sur des ordres de grandeur. Si un objet s'écarte radialement de cet objet il va perdre de l'énergie. On peut calculer l'énergie perdue en intégrant à partir de la loi de Newton en intégrant de R à l'infini. Cette énergie, il va la prélever sur son énergie cinétique initiale. Si celle-ci est inférieure à l'énergie d'extraction, de la distance au centre R à l'infini, l'objet retombera sur l'astre, sinon il s'évadera.

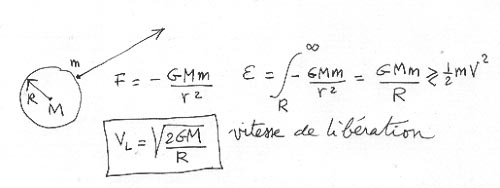
C'est une formule toute simple qui nous fera de l'usage. Signalons au passage que la valeur de la constante de la Gravitation est :

G = 6,67 10^-11 MKSA

Si vous voulez vous amuser à mettre une poignée de points-masses quelque part dans l'espace de votre ordinateur cela vous permettra d'avoir un ordre de grandeur des vitesses à ne pas dépasser. Imaginez que vos points représentent une sorte d'essaim d'abeilles. Vous sommez les masses et vous calculez sur cette base la vitesse de libération. Si vous donnez à vos particules une vitesse bien supérieure votre amas va "s'évaporer". Si la vitesse est plus faible, ah, ma foi, il faudra voir.

Que se passe-t-il donc dans une galaxie ? Nous ne pouvons qu'essayer de le deviner. Nos durées de vie sont beaucoup trop faibles pour espérer vérifier quoi que ce soit à l'échelle des temps cosmiques. Que notre galaxie effectue la moitié d'une rotation, dans le passé, et nous voilà déjà l'âge des dinosaures...

Il va falloir comprendre comment ces "univers-îles se forment. J'ai des idées sur la question et c'est pour cela que nous allons faire route ensemble. Sans vous, qui programmez, qui réussirez à faire travailler vingt, cinquante, cent ordinateurs ensemble, je ne pourrai rien. Douze années se sont écoulées depuis nos premiers résultats, sans qu'un astrophysicien ne fasse le moindre pas. Le gémellaire est "hors paradigme".

Dans notre galaxie nous avons des formations que nous appelons amas globulaires. Le plus connu est M13, l'amas d'Hercule.

Amas d'Hercule

Combien d'étoiles ? Difficile de les compter. On sait seulement qu'elles sont pauvres en métaux, donc anciennes. Les étoiles plus récentes sont de seconde génération et se son formées avec des rejets émanant d'autres étoiles, en particulier des supernovae qui synthétisent les éléments lourds. Le métal de votre plombage dentaire a été jadis synthétisé dans une supernova, ou peut être même dans plusieurs, qui sait. Les astronomes disent que l'amas d'Hercule contiendrait "plusieurs centaines de milliers d'étoiles". En prenant comme masse moyenne la masse du Soleil vous pouvez calculez les valeurs de la vitesse d'évasion Avec cent mille étoile ça fait dans les 4 km/s. Avec 400.000 étoiles on monte à 7,8 km/s. Avant même de faire des mesures par effet Doppler on peut déjà se dire que les vitesses des étoiles dans cet amas doivent être sensiblement inférieures à cette vitesse de libération, sinon cette formation se serait dissipée depuis longtemps.

Les amas globulaires sont en fait de petites galaxies sphéroïdales. Rien qu'à les regarder on peut se dire qu'ils ne tournent pas sur eux-mêmes. Sinon ils prendraient une forme elliptique.

Je sais ce que vous vous dites. Vous aimeriez bien mettre un amas globulaire dans votre ordinateur et essayer de jouer avec, en schématisant la bête avec 5000 points-masses. Oui mais, quelles conditions initiales mettre ? C'est là que je pourrais vous donner des indications assez précises car ces objets sont pratiquement les seuls pour lesquels nous disposons d'un modèle théorique self-consistent, issu d'un mariage entre l'équation de Vlasov et l'équation de Poisson. Si vous avancez dans ces simulations vous me contraindrez à délaisser un peu l'égyptologie et les techniques de navigation dans l'Ancien Empire et au Pérou, à l'époque où nous, les Gaulois, vivions encore dans des cavernes et à exhumer des trucs d'il y a trente ans. J'avais prévu d'abandonner, mais vos initiatives font que je ne peux pas me défiler. Alors, si nous continuons je vous installerai un jour un cours de DEA d'astrophysique théorique, tel que vous n'en trouverez dans aucune université ou laboratoire. Les souvenirs remontent. C'est très joli. Pour moi c'était simplement il y a trente ans. Il doit y avoir une communication J.P.Petit - G.Monnet, à un colloque sur la dynamique galactique à l'Institut des Hautes Etudes de Bures sur Yvette. 1972, je crois. On fait les calculs dans un espace à sept dimensions (position - vitesse - temps) , avec des matrices "dyades". Avec les matrices c'est très "compact". Sans, c'est .. inextricable.

Bon, ne nous dispersons pas. Il faut que je me concentre. Je suis fatigué et "les services" me préparent un nouveau sale coup. J'ai été prévenu. Ces gens sont des ordures. Ils ont écrasé déjà trois personnes de ma connaissances, en les ruinant. La justice est très coopérative pour ces affaires de raison d'état. Pour le dernier on a même fabriqué de fausses preuves. Il dérangeait.

Revenons à nos moutons. Que se passe-t-il dans un tel amas ? Pourquoi perdure-t-il ? Parce qu'il est "quasi non-collisionnel".

Que veut dire ce mot ? C'est un concept qu'il faut amener. Qu'est-ce que ça veut dire "collisionnel" ? Est-ce à dire que des étoiles se percuteraient ? Non. Considérons un ensemble d'étoiles plus vaste : notre propre galaxie. Cent ou deux cent milliards d'étoiles. Un système pratiquement non-collisionnel, si on excepte la partie qui est près du centre. Qu'entend-t-on par "collision" ? Le mot anglais est "encounter", rencontre. Il est plus proche de ce qu'on veut exprimer. Prenez une masse ponctuelle M, bien lourde, donc qu'on peut considérer comme fixe par rapport à un objet de masse m en approche. Ca, vous pouvez le simuler sur votre ordinateur et voir ce qui se passe. Un problème simple et amusant. Vous mettez la masse M bien au centre et vous tirer cette mini-masse m à l'horizontale. Deux paramètres : la distance à laquelle cette masse passerait au plus près, s'il n'y avait aucune interaction. Nous l'appelleront paramètre d'impact b. C'est le terme consacré. Second paramètre, la vitesse avec laquelle vous tirez ce plomb de chasse. Nous l'appellerons g.

Imaginons d'abord que nous tirions cette petite masse à même vitesse g mais avec des valeurs différentes du "paramètre d'impact" b . On imaginera des trajectoires hyperboliques et obtiendra ceci :

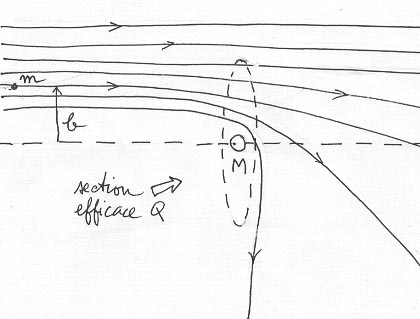
Déflexions à vitesse d'approche constante

On voit qu'à partir d'une certaine distance la déflexion devient insignifiante. Cela permet de définir ce qu'on appellera une "section efficace de collision" Q = p b^2. On voit également, en tirant la masse m avec des vitesses différentes que cette section efficace dépend de la vitesse : Q = Q(g)

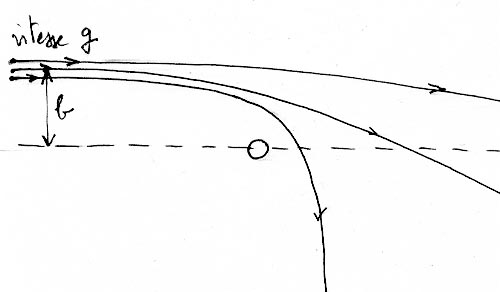
Déflexions pour des mêmes valeurs du paramètre d'impact b

On pourrait définir la section efficace de collision comme la valeur du disque de rayon b tel qu'avec cette valeur du paramètre d'impact la déflexion soit de 1°. On voit que pour une même valeur de b, plus la vitesse d'approche g est grande et plus faible est la déflexion. Ainsi Q(g) sera une fonction (rapidement) décroissante de g. Je mets en place là, au passage, quelques concepts issus de la théorie cinétique des gaz. Nous avons considéré ici des masses dissemblables, mais nous aurions pu tout aussi bien prendre des masses identiques, ou très voisines et nous aurions obtenu les mêmes schémas, à conditions de nous placer dans un référentiel lié à l'un des objets, lequel est alors traité comme un objet fixe, l'autre étant en approche. Dans un gaz la vitesse g sera alors la vitesse d'agitation thermique dans le milieu.

Nous envisagerons d'aborder des problèmes de dynamique galactique où le milieu galactique sera assimilé à un gaz, à un fluide. Dans une galaxie il y a tellement d'étoiles (deux cent milliards pour les spirales à plusieurs milliers de milliards pour les elliptiques) que cet ensemble peut être assimilé à un fluide continu, à un gaz dont les molécules seraient des étoiles. Maintenant que nous cernons un peu mieux le concept de section efficace de collision, qu'est-ce qui fait la différence entre un milieu collisionnel et un milieu non-collisionnel ?

Prenons un milieu collisionnel : l'air que vous respirez. Il est exempt de "processus collectifs", du style gravitation ou action sous l'effet de forces de type électromagnétique. Ca n'est pas non plus un plasma. Les seules forces qui sont à l'oeuvre sont liées aux rencontres, au croisement entre molécules. Les "sections efficaces de collision" sont très faibles, de l'ordre de 10^-20 mètre carré, une unité qu'on appelle le barn. Mais les molécules sont aussi très proches. Elles se baladent dans de l'air aux conditions standard à 400 m/s, une vitesse proche de la vitesse du son. Normal, le son procès par collisions, de proche en proche. Lire l'Aspirisouffle (Alias "Si on volait") dans la collection Lanturlu. Une bonne initiation à la théorie cinétique des gaz, en BD. On dégage alors deux concepts, celui de fréquence de collision et celui de libre parcours moyen. Ce sont des choses assez simples à faire émerger. Nous réserverons la lettre C pour désigner la vitesse d'agitation thermique, par rapport à un mouvement d'ensemble. En gras, ça veut dire vecteur, en maigre c'est le module du vecteur.

V est la vitesse d'une molécule par rapport à un référentiel fixe. C'est la "vitesse absolue".

<V> est la moyenne des vitesses absolue dans un élément de gaz. C'est la vitesse macroscopique.

C = V - <V> . C'est la vitesse d'agitation thermique, que les astrophysiciens appellent vitesse résiduelle. Notez tous ces termes.

C est le module de C

<C> est la moyenne du module de la vitesse d'agitation thermique. Dans de l'air dans les conditions normales ceci vaut 400 m/s.

J'en profite au passage, tant qu'à faire, pour définir la température absolue dans un gaz. Par définition c'est la mesure de la valeur moyenne de l'énergie cinétique liée à l'agitation thermique. Notez cela.

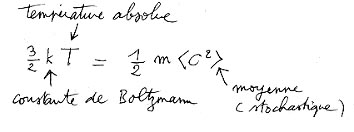
Valeur de la constante de Boltzmann, notez :

Constante de Boltzmann :    k = 1,38 10-23 MKSA

Boltzmann, un génie qui s'est suicidé parce que personne ne s'intéressait à ses travaux et ne les comprenait. A partir de là on calcule la vitesse d'agitation thermique à partir de la température absolue :

Remarque immédiate : un gaz où la vitesse d'agitation thermique est nulle est un gaz à température absolue nulle. Autre remarque : il ne peut pas exister dans le cosmos de milieu gazeux qui soit à une température inférieure à cette du "four cosmique" : 2,7 ° K. Traduisons cela en terme de vitesse d'agitation thermique d'un atome d'hydrogène. Notez :

Masse d'un atome d'hydrogène :    1,17 10^-27 kilo

On trouve 260 mètres par seconde. C'est la vitesse moyenne d'agitation thermique dans une nuage d'hydrogène qui est à la température du four cosmique à 2,7 °K. C'est pas nul.

On peut calculer la fréquence de collision (d'interaction entre une molécule est ses voisines). Pour cela on imagine une molécule qui se balade à la vitesse <C> en trimballant, comme un parapluie, sa section efficace de collision. Elle va balayer pendant le temps dt le volume : Q <C> dt . Dans ce volume il y a

n Q <C> dt molécules, n étant le nombre de densité (nombre par mètre cube).

On obtient la fréquence de collision. Calculons-là dans l'air que vous respirez. Dans 22,4 litres d'air dans des conditions normales de température et de pression il un nombre de molécules égal au :

nombre d'Avogadro :   6,22 10²³

soit 2,77 10²⁵ molécules par mètre cube d'air. En prenant une section efficace d'un barn (&&& un lecteur me confirmera cette valeur que j'extraie d'une mémoire déjà assez encombrée) on obtient une fréquence de collision de 8 10⁷ par seconde.

En prenant l'inverse

on obtient le temps de libre parcours moyen : 1,25 10^-8 de l'ordre d'un centième de microseconde. En multipliant ce temps par la valeur moyenne de la vitesse d'agitation thermique on obtient le libre parcours moyen :

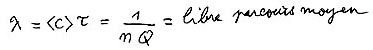
On trouve 5 10^-6 mètre : cinq microns.

Les collisions, les interactions entre molécules tendent à faire passer le gaz en état d'entropie maximale, à l'état d'équilibre thermodynamique locale (la théorie cinétique des gaz permettra de vous faire comprendre ce qu'est l'entropie, dans le cas d'un gaz, et même de la calculer pas après pas). Ce concept est important car on s'en servira pour définir des conditions initiales au point de vue des vitesse d'agitation thermique, qu'on pourra aussi vitesses résiduelles dans un milieu constitué de masses m, ces masses pouvant éventuellement être :

- Des étoiles

- Des nuages de gaz interstellaire

- Des condensations quelconques de matière ou d ematière gémellaire

- Des .. galaxies, assimilées à des "points-masses" dans des amas de galaxies (1000 individus dans les amas Coma et Virgo).

Quand on fera des calculs, ultérieurement, on réservera les lettres ( U , V , W ) pour désigner les composantes de la vitesse d'agitation thermique C

C'est quoi, l'équilibre thermodynamique local ? C'est un état du gaz dans l'espace des vitesses où la vitesse est pondérée par une densité de probabilité Gaussienne ("distribution de maxwell-Boltzmann") qui s'écrit :

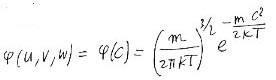
Ceci signifie que chaque composante de la vitesse d'agitation thermique devra être pondérée par la probabilité :

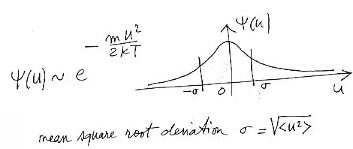
Tout cela peut vous paraître un peu compliqué, mais c'est la façon de doter des points-masses d'une distribution des vitesses de manière un peu rigoureuse, qui correspondent à un état initial d'équilibre thermodynamique. Ceux qui programmerons n'aurons peut être pas tous à faire cela. Ca n'est pas bien compliqué d'ailleurs. Mon ami Gilles d'Agostini l'a fait et ça se présente sous la forme d'un programme en Pascal qui est très conversationnel. On dirait de nos jours que Gille sl'a doté d'une bonne "interface utilisateur". Soit vous utiliserez ce programme tout fait, soit vous pourrez le modifier selon vos besoins (nous fournirons systématiquement tous les codes -sources). Et en tout cas vous comprendrez alors le sens d'un sous-programme créant la distribution des vitesses, ce qu'il fait.

A la lumière de tout ce qui vient d'être dit qu'est-ce qu'un milieu collisionnel ? C'est un milieu où le temps de libre parcours moyen est faible devant les temps caractéristiques des phénomènes étudiés, ou les libre parcours moyens sont faibles devant l'ordre de grandeur des longueurs caractéristiques des objets ou phénomènes considérés. Un Airbus, un Mirage III vole dans un fluide collisionnel.

Précisons que ce temps de libre parcours moyen est le temps caractéristique de retour à l'équilibre thermodynamique. En d'autres termes un milieu en non-équilibre retourne dans cette situation de Maxwell-Boltzmann en quelques collisions. S'il y a retour à l'équilibre c'est qu'il y a eu situation de non-équilibre. En mécaflu classique la situation de non-équilibre est typiquement une onde de choc. A travers cette onde de choc l'air, ou un gaz, va être recomprimé et échauffé très rapidement. Imaginons une onde de choc qui accompagne un avion volant à 2000 km/h. Multiplions cette vitesse par le temps de libre parcours moyen. On obtient une longueur de l'ordre du centimètre. Ca n'est pas l'épaisseur de l'onde de choc, qui est elle de l'ordre du libre parcours moyen mais la distance sur laquelle l'air retournera à l'état d'équilibre thermodynamique. l'onde de choc est équivalente à un "coup de marteau", qui donne aux molécules une impulsion dans une direction données. Ce surcroît d'énergie cinétique est ensuite redistribué dans toutes les directions. On emploiera le mot "thermalisation". Celle-ci s'effectue à l'aide de quelques collisions. Les collision font que toute molécule "perd le souvenir de la vitesse qu'elle avait avant". Il y a ensuite échange d'énergie dans ces interaction. Tout ceci concourt à mettre le gaz dans un état d'équilibre thermodynamique local. En mécaflu ordinaire les gaz sont "à l'état d'équilibre presque partout". Partout sauf dans des volumes très particuliers et restreints : dans de minces ondes de choc, très près de parois surchauffées, etc.

Un milieu collisionnel est donc un milieu en état d'équilibre thermodynamique local, dont la distribution locale des vitesses est proche d'une distribution de Maxwell-Boltzmann.

Inversement un milieu non-collisionnel est un milieu où les temps de libre parcours (donc de temps de retour à l'équilibre) sont grands devant les échelles de temps des phénomènes considérés, où les libres parcours moyens sont grands devant les échelles de longueur. Un milieu non-collisionnel sera hors d'équilibre thermodynamique et sa fonction de distribution des vitesses différera d'une distribution isotrope de type Maxwell-Boltzmann.

Je dis cela car dans l'avenir, quand nous pourrons gérer un nombre important d epoints, en 3d, il nous sera possible de faire une évaluation de l'écart à l'équilibre thermodynamique, localement, ce qui sera une donnée fort intéressante. Le "gaz d'étoiles", dans une galaxie (comme la nôtre) constitue un milieu totalement cnon-collisionnel. Pour en arriver à cette conclusion il faut savoir évaluer une section efficace de collision lors d'une interaction à deux corps, de type gravitationnel. Ce travail a été fait par Chandrasekhar et publié en 1942 dans un ouvrage intitulé Principles of Stellar Dynamics, Dover publication, New York. Le résultat est en haut de la page 81 (coup de chance, je retrouve cet ouvrage, on je n'ai pas mis le nez depuis 30 ans, dans mon grenier).

Le "temps de relaxation" d'une galaxie est évalué par lui à 10¹⁴ années, soit dix mille fois l'âge de l'univers.

Comment interpréter ce résultat ? Prenez un volume dans notre galaxie contenant un certain nombre, suffisant pour faire une statistique, d'étoiles. Disons un millier. Nous savons mesurer les vitesses des étoiles dans notre environnement immédiat, par effet Doppler. Nous pouvons donc considérer une direction quelconque, une sorte de cône étroit et faire la statistique des vitesses des étoiles dans cette direction. On trouvera toujours grosso modo une Gaussienne. On pourra calculer dans cette direction l'écart quadratique moyen. Une distribution Gaussienne est isotrope. L'écart quadratique moyen est le même quelle que soit la direction considérée. Si on porte la valeur de cet écart quadratique moyen sur la direction considérée on obtient un sphéroïde des vitesses. Mais, autour du soleil si on porte ces résultats on obtient un ellipsoïde des vitesses. La distribution des vitesses n'est pas isotrope, loin s'en faut. C'est aussi le signe que le milieu est très non-collisionnel, que le temps de relaxation dans une galaxie est très grand.

Sphéroïde et ellippsoïde des vitesses.

Il est important de comprendre que les objets de l'astrophysique sont des structures heptadimensionelles, à sept dimensions. La structure dans l'espace des vitesses et aussi importante que celle qu'on voit, en 3d. Notre galaxie est un objet totalement non-collisionnel, c'est à dire que pour unb point-masse, seul compte de champ général. Prenons l'exemple de notre Soleil. La probabilité pour que sa course dans la galaxie soit soudain infléchie par un passage à proximité d'une autre étoile doit être considéré comme un événement à propbabilité nulle. Notre Soleil "ne sait pas que les autres étoiles existent". Il se balade dans le "champ général". Par contre, et on abordera ce problème à travers les simulations, les étoiles sont sensibles à des passages à proximté de masses de gaz interstellaire. Tout cela n'a jamais été correctement modélisé, tout simplement parce que les astrophysiciens ne comprennent pas vraiment les mécanismes qui sont à l'oeuvre dans les galaxies. Tout le problème vient du fait qu'il s'agit de "fluides" dont le comportement est totalement différent de ceux des fluides collisionnels. On peut dire qu'au plan de la théorie pure la dynamique galactique en est au point zéro. Les modèles dépendent d'un ensemble de deux éaquations : celle de Vlasov et celle de Poisson. On ne connaît qu'un nombre infime de solutions exactes, et dans des cas très particuliers. L'une d'elle, due à Eddington (1924) permet de décrire un objet à symétrie sphérique comme l'amas globulaire d'Hercule. Jetez un oeil à la figure ci-dessus. L'amas possède un ellipsoïde des vitesses qui pointe son grand axe vers le centre géométrique du système. Ce grand axe est constant. par contre les axes transverses, "maigrissent" au fur et à mesure que r croît, ce que j'ai représente sur la figure. Vous voyez qu'il n'est pas si simple de tenter de construire cet amas en tant qu'ensemble de masses en interaction, si on ne les dotent pas de vitesses d'agitation ad hoc, ce qui n'est nullement apparaît sur les photos.

En fait, les seuls animaux qui ont un système perceptif à sept dimensions sont les chaeve-souris, qui ont une perception "bi-auriculaire" à la fois en distance et en vitesse. Le laps de temps s'écoulant entre l'émission et la réception d'impulsions ultrasoniques donne la distance , précisée par la perception bi-auriculaire. La perception de l'effet Doppler donne une imagerie mentale. en vitesse. Pour les chauve-souris le monde doit avoir réellement sept dimensions, du moins c'est ainsi qu'elles le percoivent. A la limite celui des limaces n'en a que trois, parce que dimension hauteur est peut être peu importante. Si la vie intelligente avait évolué à partir de créatures comme les chauves souris le sprogrès en astrophysique auraient peut être été plus rapides. Nous avons un peu de mal à percevoir ces systèmes à N corps dans une perspective position + vitesse. Il faudra vous habituer à le faire.

Un système non-collisionnel est ... incompressioble dans l'espace à six dimensions, position plus vitesse (théorème de Liouvile) et son comportement est ... isentropique (vous apprendrez, dans les simulations, à calculer l'entropie, ce qui débouchera sur une méthode supplémentaire de contrôle de la fiabilité des calculs et permettra de parfaire la chasse aux artefacts. Les mécanismes d'échange d'énergie sont différents de ceux dont nous avons l'habitude. Conceptuellement c'est un état de la matière différent, un cinquième état qui recèle encore bien des mystères. Dans un gaz, localement, on peut toujours calculer une conductivité thermique, une viscosité. Un transfert de chaleur par conduction, un phénomène de viscosité passent pas un état local de non-équilibre, mais très proche de l'équilibre thermodynamique. Le gaz est "quasi-maxwellien". Si le fluide était totalement à l'équilibre la température serait la même partout, et les seuls mouvements autorisés seraient ceux où les transferts visqueux sont absents (rotation en corps solide, plus expansion ou contraction isotrope). Ce calcul des "coefficients de transferts" dans un gaz passe par une méthode perturbationelle, tournant autour d'un "point central", qui est l'état d'équilibre thermodynamique local. L'immense majorité des travaux théoriques en physique tournent autour perturbationnel, qui permet la linéarisation. Impossible dans un milieu non-collisionnel. C'est le non-linéaire ou rien. Aride pour le théoricien.

Il faut un nombre de points-masses relativement important pour pouvoir obtenir des résultats réellement significatifs en matière de statistique des vitesses. En 3d il nous en faudra un bon million. Tout ceci n'a jamais été fait. Au plan observationnel sachez que nous n'avons de connaissance de l'ellipsoïde des vitesse qu'au voisinage du soleil. Celui-ci possède un grand axe qui pointe, grosso-modo dans le direction du centre de la galaxie. Les axes transverses, à peu près égaux, sont inférieurs de moitié. On voir que c'est très différent du sphéroïde de la distribution de Maxwell-Boltzmann. Détail supplémentaire : ce grand axe de l'ellipsoïde des vitesses ne pointe pas exactement vers le le centre de la galaxie mais un peu à côté. On appelle cela la "déviation du vertex". Raison de cet état de fait : personne n'en la moindre idée. Ne demandez pas au couple infernal de l'observatoire de Marseille, Bosma (celui qui m'avait fait interdire de parole au colloque de Montpellier en 1999) et Lia Athanassoula, son épouse. Pour moi ces gens ne sont pas des astrophysiciens dignes de ce nom, mais des simulateurs-cuisiniers en fin de carrière, qui sont restés dans réagir pendant 12 ans face à ces idées gémellaires, alors qu'ils avaient tous les moyens de calcul pour s'y mettre (qui ont coûté sacrémengt cher à lm'obs pendant 20 ans avez zéro résultats). C'est simplement lamentable. Même chose pour la normalienne Françoise Combe, de l'observatoire de Paris.On s'emmerde, dans ces milieux d'astrophsiciens, depuis plus d'un quart de siècle. Aucun n'a la moindre idée, ni le ... moindre résultat à produire. Il est temps de confier cela à des amateurs, cochés par un retraité.

Il y aurait même des travaux de théorie pure, avec recherche dans un contexte gémallaire de solutions exactes, à initier, en reprenant ces techniques d'attaques des systèmes d'équation par techniques tensorielles. Mais là, tout serait à faire et vous ne trouverez dans aucun DEA d'enseignements qui vous permettent d'attaquer ces questions. ce savoir-faire s'est totalement perdu. De nos jours, les séances de travaux dirigés consistent à (mal) masturber un ordinateur.

J'ai dit que les galaxies étaient des systèmes non-collisionnels. Comment peut-on espérer simuler de tels systèmes avec un nombre relativement faible de points ? Comment éviter que des "mauvaises rencontres" se produisent ? L'astuce est simple. Il suffit simplement de décider que quand deux corps s'approchent à une distance inférieure à la "distance de collision", celle qui créerait une déflexion trop importante l'insteraction disparaît, devient nulle. Ainsi chaque point masse "ne voit pas les autres points masses" quand il n'est approche de trop près.

Revenons sur ce thème de l'évolution de s systèmes à N corps. En astrophysique on tombe sur une situation particulière. Le système n'est pas contenu dans un récipient. Prenons l'exemple d'un système collisionnel. Les "collisions" ou interactions de proximités entre deux éléments vont faire tendre le système vers un état d'équilibre thermodynamique, une distribution des vitesses de Maxwell-Boltzmann, centrée autour d'une valeur moyenne de la vitesse d'agitation. Ci-après l'allure de la densité de probabilité sur le module C de la vitesse d'agitation.

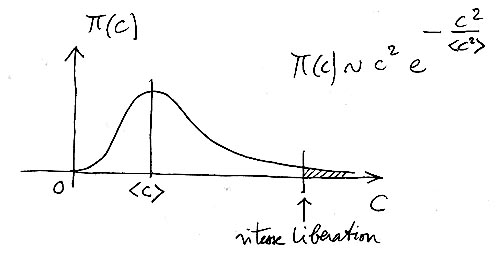
Densité de probabilité sur le module de la vitesse d'agitation

Cela implique qu'il y aura des éléments à vitesse nulle ou très faible, mais aussi des éléments rapides. Il n'y a, mathématiquement, aucune limite à la vitesse. Si l'air que vous respirez est composé de molécules dont la vitesse moyenne d'agitation thermique est de 400 mètres par seconde, cela signifie que dans vos poumons cohabitent aussi des molécules croisant à 20 m/s comme d'autres à 1500 mètres par seconde. En astrophysique l'existence de ces particules rapides pose un problème. Faut d'une paroi sur laquelle elles puissent rebondir, si leur vitesse dépasse la vitesse de libération, elles partent sans jamais revenir. Ca sera le cas pour toutes les particules de la "queue de distribution boltzmanienne", à droite, hachurée.

Si les amas stellaires globulaires étaient des systèmes coillisionnels ils auraient perdu leurs étoiles depuis belle lurette et auraient disparu. Or ils sont toujours là. En fait ce sont des systèmes "hors d'équilibre thermodynamique". Mais au coeur des amas, plus denses, se situe un régime où des collisions de produisent, qui alimentent l'amas en étoiles ... lentes et rapides. ces étoiles rapides s'évadent. Le Français Hénon, de Nice avait pu calculer il y a 25 ans le taux d'évaporation des amas et montré que leur durée de vie était proportionnelle à leur masse.

Les amas globulaires sont constitués par les étoiles les plus anciennes possibles. Il n'y en a pas de plus âgées. Question : les galaxies se sont-elles formées en tant qu'amas de gaz ou par accrétion d'objets comme les amas globulaires. J'aurais tendance à opter pour la seconde solution. Mais seules des simulations très élaborées permettraient de consolider cette idée. En effet la naissance des galaxies est indissociable de l'évolution du cosmos dans son premier âge. On sait (lire ma BD Big Bang, série des Lanturlu) que jusqu'à ce que l'univers soit âgé de 100.000 ans matière et rayonnement sont fortement couplés. La matière ne peut former des condensâts. Le rayonnement se trouve piégé. Tout simplement parce que le libre parcours des photons est très faible. Ils sont absorbés, tréémùis, sans cesse. Il en est de même dans le Soleil. Un photon créé au coeur du soleil, associé à un processus de fusion ne saurait s'évader comme ça. L'énergie de fusion ne diffuse que lentement à la surface du Soleil. Ces photons représentent une certaine énergie par unité de volume, une certaine pression de rayonnement. Si une main de géant "comprimait le Soleil", les photons qui sont "emprisonnés dedans", c'est à dire pris dans des cycles incessants d'absorbtion et de réémission seraient entraînés dans ce mouvement de compression.

Mais la composante radiative de la pression de rayonnement à la pression régnant dans le Soleil est faible, négigeable. Ca n'aurait aucun effet. Il n'en est pas de même avant le découplage. L'hydrogène, à plus de 3000° étant complètement ionisé de trouve étroitement couplé au rayonnement. Pourquoi ? Parce qu'un gaz ionisé est un milieu très absorbant vis à vis d'un rayonnement électromagnétique. Les "antennes" qui captent cette énergie ce sont les électrons libres, nombreux si l'hydrogène est ionisés. les photons, ondes électromagnétiques, communiquent leur énergie aux électrons libres, qui la réemmettent par la suite. Ces électrons libres sont beaucoup plus sensibles au rayonnement électomagnétique quand ils sont libres que quand ils sont liés (au noyau, en constituant un atome). Matière et rayonnement restent étroitement couplés jusqu'à ce que l'hydrogène se désionise, à une température inférieure à 3000°K.

A tout moment, dans un milieu de densité r et de température T il y a potentialité de voir apparaître des grumeaux, des "clusters" (peu importe le nom qu'on leur donne). On parlera de ce mécanisme, l'instabilité gravitationnelle, ou instabilité de Jeans dans le dossier suivant. Si R est le facteur d'échelle de l'univers, alors les grumeaux qui tendent à se former ont un diamètre L_j qui croît la puissance 1/2 de R (on le montrera). A l'intérieur de ces sphères de diamètre L_j se trouve une masse M_j, la masse de Jeans. Au moment du découplage cette masse de Jeans se trouve être précisément proche de la masse des amas globulaires. Donc en toute logique ce sont ces objets qui devraient s'être formés les premiers. Puis il se seraient rassemblés par un nouveau processus d'accrétion. Mais les choses sont loin d'être simples car ce processus de naissance des galaxies se serait fait en conjugaison avec la présence de la matière gémellaire environnante (qui, elle, ne donnerait pas naissance à des "étoiles gémellaires). On parlera alors d'instabilités gravitationnelles conjointes.

La galaxie primitive pourrait être formée d'amas donnant naissance, très vite, à des centaines de milliers d'étoiles. Seuls les amas les plus massifs survivent, conformément aux idées d'Hénon. Ceux qui ont des masses plus faibles se dispersent. On pense que les étoiles des générations suivantes son nées et continuent de naître également par paquets, en formant des amas de quelques centaines d'individus. Ces amas ont alors des durées de vie faibles. De plus ils sont constitués d'étoiles de masses variées. Il ne s'agit que de spéculations, mais un "amas type" où le Soleil aurait pu naître aurait pu être composé de quelques étoiles très massives (20 masses solaires et plus), qui évolueraient très vite en supernovae et exploseraient, ensemençant l'amas en éléments lourds, qui donneront les nuages proto-planétaires. Ca, plus des étoiles de type solaire, plus une tapée d'étoiles naines, pense-t-on.

A ce stade se situe un phénomène qu'il faudra modéliser avec des simulations : l'effet de fronde. D'Agostini s'est déjà amusé a étudier le phénomène en lançant un objet de faible de masse vers un gros, sous un bon angle. L'accélération est alors spectaculaire. Il faudra illustrer cela par des gif animés. En règle générale les amas d'étoiles commencent par se constituer en ensembles collisionnels. On aura donc une tendance vers une distribution de Maxwell-Boltzmann, avec des objets rapides, qui vont s'évader parce qu'ils acquièrent une vitesse dépassant la vitesse de libération.

Phénomène supplémentaire : les objets légers prennent plus de vitesse. On peut voir cela comme une conséquence de l'effet de fronde. Mais on peut voir cela aussi comme une tendance à l'équilibre thermodynamique. En effet considérons une enceinte fermée contenant des molécules de masses dissemblables M1 et m2 . Ces deux populations ont des températures absolues qui suivent la relation :

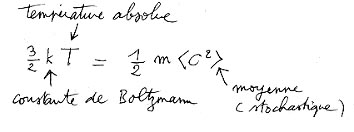
En état d'équilibre thermodynamique il y a équipartition des énergies. Les températures de toutes les espèces deviennent égales, puisqu'elles sont par définition les mesures des valeurs moyennes des énergies cinétiques d'agitation thermique. Les rapports des vitesses moyennes d'agitation seront comme l'inverse de la racine carrée du rapport des masses :

Si on considère par exemple un plasma d'hydrogène, un mélange d'électrons et de protons et si ce mélange est en état d'équilibre thermodynamique alors la vitesse moyenne d'agitation thermique des électrons sera 43 fois plus élevée que celle des protons.

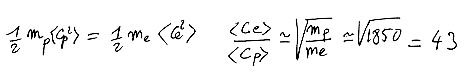
On étudiera, dans l'éventail des simulations envisagées, le comportement d'un jeune amas stellaire, de quelques centaines d'étoiles, juste après sa constitution. Il est alors collisionnel et constitué par des proto-étoiles de différentes masses. Si cet amas était dans une enceinte, l'ensemble tendrait vers l'équilibre thermodynamique. On aurait alors un mélange où les proto-étoiles de faibles masses auraient des vitesses résiduelles plus importantes que les étoiles massive. En règle générale les amas éjectent en premier les objets les plus légers.

Plus il y a d'objets éjectés et plus la masse de l'amas diminue, de même que la vitesse d'évasion qui lui est associée (qui varie comme la racine carrée de la masse). Il y a alors auto-accélération du phénomène. Les amas globulaires perdent des étoiles parce qu'en leur centre des collisions (au sens d'interactions binaires) créent des étoiles rapides, qui s'évadent. Dans le cente de notre galaxie les étoiles sont plus proches et le système est faiblement collisionnel. Il y a donc création d'étoiles rapides. Mais leurs vitesses resteraient insuffisantes pour qu'elles quittent la galaxie. Ces interactions les envoient dans toutes les directions, gonflent le "bulbe". On expliquera aussi pourquoi les étoiles jeunes, émettant de l'UV sont dans le disque de gaz. C'est là qu'elles naissent. Puis, au fil de rencontres avec des masses de gaz interstellaire elles sont envoyées hors du plan de la galaxien, venant enrichi de "halo".

Ce phénomène d'accélération des objets légers par les objets lourds a de multiples facettes, dans le cosmos, à toutes les échelles. Dans un système solaire en formation il enverra au loin de nombreux débris qui deviendront astéroïdes et comêtes. Quand nous aurons assez de points-masses pour pouvoir gérer des systèmes à plusieurs populations nous pourrons mettre en évidence des tas de choses intéressantes.

5 mai 2004 : les quelques images que j'ai reçues sont très encourangeantes. Il y a des gens au travail. Mais les choses sérieuses ne viendront que quand on aura ssez de points-masses pour décrire une galaxie avec plusieurs populations. Toujours au rayon "tendance vers l'équilibre thermodynamique" il faut savoir que celui-ci entraîne l'équipartition des énergies, non seulement de translation, mais de rotation. Une "molécule" peut posséder une énergie de translation 1/2 m V², mais aussi une énergie de rotation 1/2 I w², où w est son moment d'inertie. Dans un gaz on aurait des valeurs moyennes < 1/2 m V² > et < 1/2 I w² > . En état d'équilibre thermodynamique ces deux quantités sont égales. C'est l'origine du mouvement de rotation des étoiles sur elles-mêmes, ou du mouvement de rotation des galaxies. Quand ces deux entités se forment, elles sont "à touche touche" et forment un système collisionnel. Tout tend à faire s'évaporer un jeune amas d'étoiles, ou à le disloquer, par effet de marée. L'expansion éloigne les galaxies les unes des autres. Quand la nôtre s'est formée, Andromède était à touche-touche.

Ces collision dans les systèmes primitifs expliquent également que le moment cinétique du système solaire soit concentré dans Jupiter et non dans le Soleil. Vestiges des collisions entre proto-systèmes solaires encore liés dans l'amas originel. Nous simulerons tout cela.

Retenez une idée, que les astrophysiciens perçoivent mal, ou pas du tout. Le cosmos est un système en état hors d'équilibre, partout. Nombre de ses aspects découlent d'une tendance vers l'équilibre thermodynamique, qui a été stoppée par l'expansion ou la dispersion des "membres du club" (étoiles, galaxies).Le premier exemple est la synthèse de l'hélium, datant de l'époque où l'univers n'était qu'une immense bombe à hydrogène. Figée par l'expansion. Etc. Les amas de galaxies étaient fortement collisionnel, d'où l'origine du mouvement de rotation des galaxies, tout simplement. Maintenant ils le sont encore, plus faiblement.

A propos, c'est Fritz Zwicky qui a créé le terme missing mass, masse manquante. Il était relativement facile d'évaluer la masse totale dans un amas de galaxies. D'où la valeur de la vitesse d'évasion, avec une formule donnée plus haut. Zwicky s'aperçut que les galaxies avaient "des vitesses d'agitation" dans l'amas supérieure à cette valeur. Quelque chose devait fonc les tenir groupées. Je suis bien d'acord, mais mon interprétation diffère de celle qui se formule, classiquement, en terme de matière sombre.

Dans les amas, les galaxies baignent dans du gaz à très haute température : de l'hydrogène à un million de degré. Si cet hydrogène ne retombe pas sur les galaxies, c'est que la vitesse des atomes excède la vitesse de libération des galaxies, prises individuellement. Donc il y a une valeur minimale. Prenez la masse d'une galaxie. Vous trouverez ça dans le dictionnaire d'astronomie de Larousse. Calculez la vitesse d'évasion correspondante. Calculez la température d'un gaz d'atomes d'hydrogène dont les composants auraient une vitesse d'agitation thermique égale ou supérieure à cette valeur. Vous trouverez ces températures.

Ces atomes se rentrent dedans, de temps en temps. L'ordre de grandeur de l' énergie émise correspond à :

1/2 m < C² > = 3/2 k T = = e V

e = charge de l'électron : 1,6 10^-19 coulomb

A droite, l'évaluation du rayonnement en électrons-volts. Vous trouverez que ces collisions génèrent des émissions dans la gamme des rayons X. En connaissant la section efficace de collision électron - proton (le milieu est évidemment totalement ionisé) et en sachant que ça émet, vous pourrez trouver une valeur minimale de la densité de gaz. En connaissant le flux de rayons X on peut calculer la densité d'hydrogène chaud. Juste ... en réfléchissant.

D'où vient cet hydrogène chaud ? A mon avis de l'époque où les galaxies venaient juste de se former et de l'émission des étoiles de première génération, qui a "fait four". Les atomes prenant des vitesses supérieures à la vitesse de libération sont partis sans espoir de retour. Les elliptiques se sont comportées comme de tels fours qu'elles ont perdu tout leur gaz. Les "spirales", plus légères, se sont entourées d'un halo diffus de gaz. Elle se sont muées en "oeuf sur le plat à 3 dimensions". Au centre, le "jaune" : les étoiles primitives, dont font partie les étoiles des 500 amas globulaires qui se distribuent selon un système à symétrie sphérique, indication selon laquelle cet ensemble ne tourne pas. Et c'est ce qu'on observe. Si cet ensemble tournait il serait aplati, comme les elliptiques. Cet ensemble d'amas globulaire est donc une image fossile de notre galaxie, qui avait tenu son gaz à distance. Comme à l'époque les galaxies des amas formaient des systèmes collisionnels, les "oeufs sur les plat 3d" se frôlaient. Ca mettent les "blancs" en rotation. D'où l'origine du mouvement de rotation du gaz dans les spirales.

Ce gaz s'est refroidi par rayonnement. Mais comme il ne pouvait pas évacuer le moment cinétique acquis, il s'est transformé en crèpe plate. Ca alors donné naissance à des étoiles de seconde génération, des "étoiles du disque", dite "de population II", les étoiles anciennes étant "de population I". Ces étoiles, issues de ce gaz résisuel, ont orbité dans le plan de la galaxies. Puis les "collisions", les rencontres ("encounters") avec des masses de gaz ont entraîné un début de "thermalisation" de cette sous-population (redistribution de la vitesse dans toutes les directions). C'est à dire que ces étoiles ont acquis une "composante en z" de vitesse et ont gagné un peu de vitesse par effet de fronde. Elles ont commencé à quitter le plan diamétral de la galaxie. Mais là, rebelote, la fréquence des rencontres avec les masses de gaz a baissé, puisque ces étoiles séjournaient moins longtemps dan la crèpe plate de gaz. Ainsi le phénomène qui les faisait tendre vers un équilibre thermodynamique (entre ce 2° gaz d'étoiles "population II" et un "gaz" constitué par d'énormes masses d'hydrogène) a engendré un phénomène (le fait de leur faire quitter la zone proche du plan diamétral où elles avaient des chances d'être accélérées) qui a freiné cette course vers l'équilibre thermodynamique (qui impliquerait l'égalisation des températures absolues des différents composants). Création d'un nième état hors équilibre thermodynamique.

Dossier suivant : l'Instabilité gravitationnelle.

Retour vers le sommaire du projet Epistémotron

Retour vers Nouveauté             Retour vers Guide                 Retour vers page d'Accueil

Nombre de consultations de cette page depuis le 5 mai 2004 :