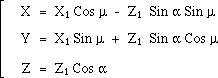...Ce travail a une histoire. Jusqu'à ce que paraisse mon album le Topologicon, aux Editions Belin, dans la série des Aventures d'Anselme Lanturlu, en 1985, les représentations de la surface de Boy, dans les ouvrages spécialisés, étaient peu nombreuses. On trouvait ici et là des photographies de modèles réalisés soit en plâtre, soit en grillage à poules. Charles Pugh, du département de mathématiques de l'université de berkeley, est le spécialiste mondial incontesté du grillage à poules. C'est d'ailleurs avec ce matériau qu'il obtint un prix, financièrement important, en réalisant les maquettes décrivant le retournement de la sphère selon Bernard Morin, maquettes qui furent ensuite digitalisées par Nelson Max pour être transformées en un film qui traîne dans tous les départements de maths du monde entier.
...Mais je trouve que le grillage à poules reste un matériau peu noble, surtout pour ces sujets scientifiques haut-de-gamme. Ayant fait la connaissance d'un plasticien nommé Max Sauze, je m'initiais à la technique du fil de fer cuivré, à la fois souple et rigide, que Max soudait avec dextérité, en se débrouillant pour ne pas trop le chauffer, pour que cela ne crée pas dans le matériau des tensions parasites.
...Mon ami Jacques Boulier, Alias Vasselin, était alors professeurs aux Beaux Arts d'Aix en Provence. Un année il me proposa de remplacer un de ses professeurs, parti à l'étranger, ce que je fis, assurant un service à mi-temps avec Sauze. Pendant que j'inventais les objets, Max les soudait. Nos étudiants, tournant autour de nous, intrigués, s'efforçaient de nous imiter de leur mieux. Cette année-là cette aile de l'école des Beaux Arts d'Aix en Provence était devenue une sorte d'usine de production en série de surfaces mathématiques.
...Si vous voulez vous y mettre, ça n'est pas compliqué. Il vous faut un rouleau de ce fil de fer cuivré, disons d'un mm et demi de diamètre, deux maximum, et une pince coupante. Avec cela vous pourrez figurer les deux familles de courbes qui composent n'importe quelle surface.
...Le problème est de réussir à modeler convenablement ces objets. Pour ce faire, il est bon de pouvoir faire glisser les points de jonction, là où les méridiens" et les "parallèles" se croident. Une bonne solution consiste à ligaturer tout simplement les deux fils de métal avec du fil à coudre. C'est assez serré pour donner à l'objet de la tenue, mais assez glissant pour permettre déformations et ajustements.
...Ca n'est que quand vous estimez que l'objet est mathématiquement conforme à vos souhaits que vous pouvez le confier à quelqu'un qui manie la brasur à l'argent avec dextérité et qui saura souder en ne chauffant pas les tiges, ce que savait faire Max avec un art consommé.
...J'amenai un jour un prototype de surface de Boy, ayant découvert comment les péridiens et les parallèles devaient s'agencer. Apparemment, on pouvait se débrouiller pour que les méridiens ressemblent à s'y méprendre à une famille d'ellipses.
...Max recopia l'objet avec soin. Je débarquai alors chez Souriau. Son fils (qui n'eût jamais la patience de terminer sa licence de physique) s'amusait avec l'Apple II de son père. Je lui lançai :
- Jérôme, est-ce que tu aurais envie d'avoir une publication de maths pures à ton nom ?
- Ma foi, pourquoi pas ? Qui faut-il tuer pour cela ?
- Personne. Tu vois cet objet. Prends un rapporteur, mesure ces ellipses et essaye de nous construire une représentation semi-empirique de cette surface.
- On peut toujours essayer, donne...
...Deux jours après, c'était fait. L'article fut rapidement accepté aux comptes Rendus de l'Académie des Sciences de Paris et publié sous nos deux noms : J.P.Petit et J.Souriau
...Mais comme le père s'appelle Jean-Marie et le fils Jérôme, tous les mathématiciens sont convaincus que c'est un travail que nous avons fait ensemble, Souriau père et moi.
...Le tracé de la surface sur ordinateur, à l'aide d'un petit programme BASIC de quelques lignes surprit grandement des tas de mathématiciens, qui s'attendaient à quelque chose de plus compliqué. L'affaire eut une retombée désagréable. Le mathématicien Bernard Morin avait un élève en thèse, Apéry, fils d'Apéry-père, auteur de l'ineffable théorème selon lequel la somme des cubes de nombres entiers est un nombre irrationnel. Entre autre....
...Je l'ignorai. Notre avancée inquiéta fort Morin, d'autant plus que je lui affirmai à l'époque naïvement que cette méthode devrait permettre de décrire la surface à quatre oreilles qui l'avait rendu célèbre, celle qui avait été construite avec son grillage à poules par Pugh, puis digitalisée par Max, etc..
Morin fronça les sourcils :
- Non, c'est impossible ! ....
...On verra cela plus tard. Je reste persuadé du contraire. Mais cette phrase était le pendant de la célèbre réplique que lança Archimède au soldat romain, venu le déranger dans ses cogitations
- Noli tangere circuleos meos !
En français "ne touche pas à mes cercles !".
Là, c'était plutôt du genre "ne touche pas à mes ellipses !"
...Par la suite Apéry exploita ma découverte, selon laquelle on pouvait doter la surface de Boy d'un système de méridiens elliptiques, pour construire la première équation implicite de l'objet :
...Morin, furieux de me voir apparaître comme un trublion dans ses propres travaux de mathématiques, imposa à Apéry de préciser, dans sa thèse, que c'était Sauze qui avait trouvé le coup des ellipses. Max ne démentit pas, mais c'est inexact. La preuve est dans ma cave : la maquette que j'amenai à Max pour qu'il la mette au propre.
...Enfin, tout ceci est assez ridicule, somme toute. Cette anecdote est là pour montrer que les mathématiciens ne sont pas plus brillants que les physiciens.
...Le polytechnicien Colonna, pionnier en matière d'images de synthèse, utilisa à tout vat nos équations, sans mentionner leur origine. Mais il existe un détail amusant, su d'aventure vous voyez sur un écran des images de la surface de Boy. Si c'est "la nôtre", elle présentera immanquablement trois légers "plis" près de son pôle. Un défaut d'ajustement des équations. Jérôme, de ils de Souriau, avait fait cela à la va-vite et un dernier petit coup de fer, au voisinage du pôle, n'aurait pas été de trop. Cela reste toujours faisable, d'ailleurs, pour qui voudra.
...Cette saga de la surface de Boy n'est pas close. Pour être complet, mentionnons un personnage : Carlo Bonomi, un milliardaire italien. J'avais fait sa connaissance lors d'une expédition au triangle des Bermudes (mais ceci est une toute autre histoire). Nous naviguions alors à vive allure sur son yacht, d'un luxe à vous couper le souffle, à la recherche d'un pyramide engloutie, signalée par un certain Charles Berlitz dans un de ses livres. Nous ne trouvâmes pas la pyramide, et nous faillîmes seulement être croqués par les nombreux requins qui hantaient ces lieux. Si vous avez un Atlas, l'endroit où cette fichue "Pyramide Atlante" était censée se trouver est au sud-ouest d'un récif appelé Cay Sal Balk, à cinquante miles au sud de Cuba.
...Entre deux plongées et deux soupers au caviar, je proposai à Bonomi de sponsoriser une fabrication intensive de surface de Boy. L'idée lui plut et il y eut une suite. Disons que la surface de Boy qui orne la salle de mathématiques du Palais de la Découverte de Paris a été payée par Bonomi et réalisée par Sauze. Le financier envisageait de monter une exposition en faisant réaliser les objets en fil d'or massif. Mais l'affaire n'eût pas eu de suite. Etonné par son silence prolongé, j'appelai ses bureaux de Milan. Hélas, impliqué dans le scandale de la loge P2, il avait été incarcéré, et son intérêt pour la topologie en avait souffert de manière irréversible.
...Le revêtement à deux feuillets d'une surface de Boy, image du projectif P2, est une sphère S2 ( voir le Topologicon ). Pugh a construit ce revêtement avec deux nappes de grillage à poules, objet en tous points remarquable, bien que, lai-je dit, je préfère personnellement le fil de fer cuivré et la représentation méridiens-parallèles. Mais, même en mathématiques pures :
...Avant de présenter la note, une dernière anecdote. Charles Pugh avait donc construit sept modèles en grillage à poules, ce qui lui avait valu un prix important, décrivant les étapes successives du retournement de la sphère, dont il sera question quand j'aurai trouvé cinq minutes pour loger cela sur le site, et qui avaient été suspendus au plafond de la cafeteria du département de mathématiques de l'Université de Berkeley.
...Les mathématiciens du monde entier venaient donc en pélérinage se pâmer devant cette séquence admirable en tous points. Mais une nuit, les modèles furent volés et nul ne sait ce qu'il advint de ces sept objets, par ailleurs strictement invendables. Quel recèleur aurait acepté une telle tractation ? A moins qu'un riche amateur, mi-esthète, mi-mathématicien, n'ai financé l'opération, aux fins de les entreposer dans une cave blindée, tout à sa joie de devenir le seul homme à pouvoir contempler cette huitième merveille du monde, fusse-t-elle fabriquée en grillage à poules.
...Pugh, en dépit de sa maîtrise du matériau, n'eut pas le courage de remettre une nouvelle série en chantier.
...Comme nous l'avons déjà dit en début de site, la vie même de Werner Boy reste un mystère. Après avoir inventé la surface à laquelle il devait attacher son nom, il se dématérialisa littéralement, après son départ de l'université. En dépit de ses recherches, Hilberth ne put retrouver sa trace et on ignore même où il fut enterré.
...Revenons aux mathématiques.
La note ci-après est relativement facile à lire. A partir des
formules 1 à 8 n'importe quel lycéen réveillé
pourra construire de très belles images et vérifier que les
coupes correspondent bien à la figure 5.
C.R.Acad.Sc. Paris,
t. 293 (5octobre 1981) Série 1 - 269
GEOMETRIE. - Une représentation analytique de la surface de Boy.
Note de Jean-Pierre Petit et Jérôme Souriau, présentée
par André Lichnérowicz.
On présente une représentation analytique de la surface de Boy,
permettant de tracer celle-ci.
1.INTRODUCTION.
... La surface inventée en 1901
par le mathématicien Werner Boy, élève de Hilberth, est
bien connue des mathématiciens. Elle peut intervenir comme étape
centrale du retournement de la sphère ( [1] et [2] ).
...En
1979 (J.P.P) avait construit une maquette en fil métallique, mettant
en évidence les positions que devaient occuper le slignes méridiennes
de la surface. Un second travail effectué en 1980 avec le sculpteur
Max Sauze permit de reconstruire une seconde maquette où les courbes
se situaient dans des plans et semblaient assez voisines d'ellipses. A partir
d'une telle maquette il semblait possible de construire une représentation
analytique d'une surface ayant la topologie de la surface de Boy, et dont
les méridiens soient des ellipses passant par un pôle unique.
2. COMMENT ENGENDRER LA SURFACE DE BOY A L'AIDE D'ELLIPSES.
...Situons le pôle à l'origine des coordonnées. En ce point la surface sera tangente au plan (XOY). Elle aura donc l'axe OZ comme axe de symétrie ternaire ( voir figure 1 ). Les courbes méridiennes sont donc des ellipses situées dans des plans Pm . Soit OX1 la trace dans le plan XOY d'un plan Pm . Appelons m l'angle (OX,OX1). Dans ce plan Pm situons un second axe OZ1 perpendiculaire à OX1 . Et appelons a l'angle (OZ, OZ1).
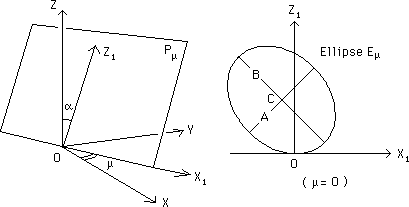
Fig.1 et Fig.2
...Le premier paramètre de cette représentation analytique sera l'angle m. On considèrera l'angle a comme une fonction de m (qui sera définie plus loin). Dans le plan Pm nous allons maintenant tracer une ellipse tangente en O à OX1 (voir figure 2) . Nous prendrons les axes de cette ellipse parallèles aux bissectrices de X1OZ1. Appelons A(m) et B(m) les valeurs des axes de cette ellipse. Cette ellipse Em sera engendré epar un second paramètre libre q .
...En résumé, on obtiendra les coordonnées X(m,q), Y(m,q), Z(m,q) du point courant de la surface.
...Dans cette approche semi-empirique, des mesures effectuées par (J.S.) sur la maquette permirent une approche des fonctions a(m), A(m) et B(m). La surface fut alors tracée par ordinateur "Apple-II" et on obtint des coupes à Z = Cte, l'examen de ces coupes permettant de déterminer l'identité topologique avec la surface de Boy. Celle-ci ne put être obtenue qu'au prix d'une expérimentation numérique (J.S.) qui permit d'éliminer les couples de singularités parasites (apparition de couples de points cuspidaux ).
...Nous avons été amenés à retenir :
(2)
(3)
![]()
![]()
(5)
![]()
...Dans ce même repère les coordonnées du point courant de l'ellipse sont
(7)
et les coordonnées
x , y , z sont données par :
(8)