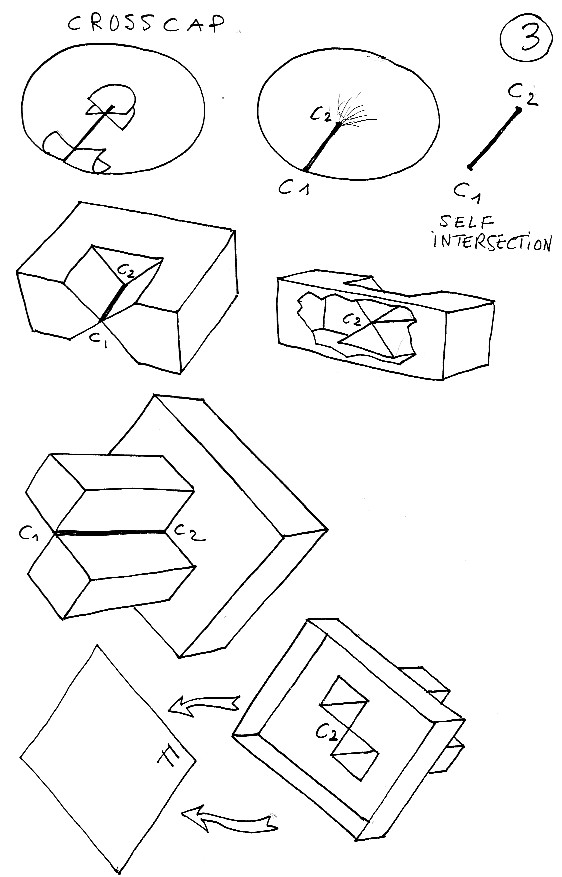
Comment transformer une crosscap en surface de Boy (droite ou gauche, au choix) en passant par la surface Romaine de Steiner.
27 septembre - 25 octobre 2003
page 2
Voilà une Cross Cap (telle que vous l'aurez découverte dans les images de réalité virtuelle). Elle comporte deux points cuspidaux qui bordent une ligne d'auro-intersection. On peut la fabriquer en pinçant un ballon avec un fer à friser. Mais vous pouvez aussi en construire des représentations polyédriques. Celle du bas nous intéressera particulièrement.

Dans cette planche 4 se situe le moment le plus difficile à appréhender. Il me paraît à peu près impossible que le premier venu comprenne ces figures en regardant simplement les dessins. Construisez ces maquettes. En clair on tire le point cuspidal C2 vers "l'intérieur de la surface" (ce qui n'a au passage aucun sens puisque, vous l'aurez sans doute remarqué immédiatement, la Cross Cap est unilatère. En insistant la surface s'auto-traverse et l'ensemble d'auto-intersection se complète, en "rondouillard" par une courbe en forme de 8. Il se crée au passage un point triple T.
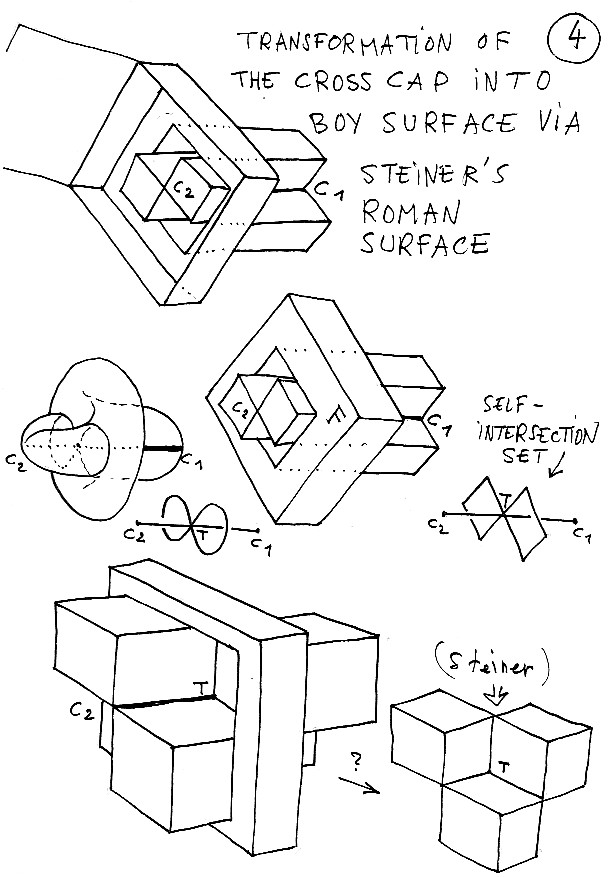
La surface est plus compréhensible sous sa forme polyédrique et, en bas, nous avons grossi certains éléments pour montrer ce qui nous incite à transformer cet objet en Surface Romaine de Steinder (voir la réalité virtuelle) dont la forme polyédrique la plus simple consiste à assembler quatre cube (ici on n'en voit que trois).
Planche 5 : Le polyédrique à gauche, le rondouillard à droite. La flèche emprunte un passage que l'on va "pincer". En bas le début du pincement.
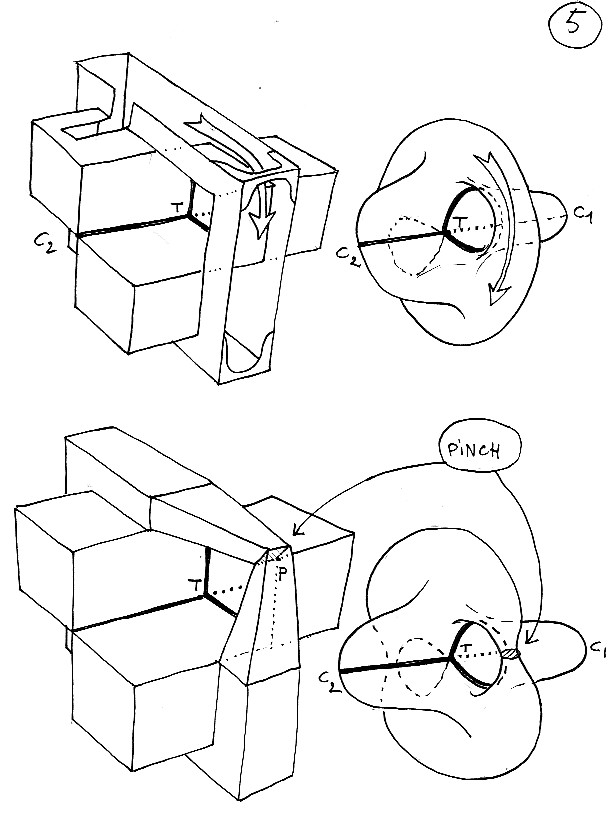
Planche 6 : le pincement est effectué en créant un point singulier B. En fait comme on pince des deux côtés, histoire de gagner du temps; il se forme deux points singuliers S1 et S1 puis deux paires de points cuspidaux. Là, sans bristol, ciseaux et ruban adhésif, vous êtes mal.
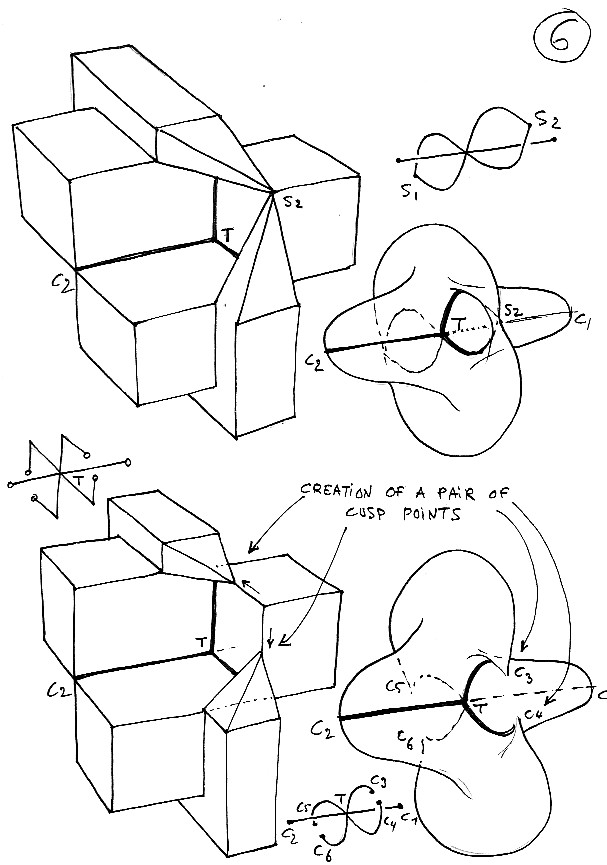
Planche 7 : on a simplement fait migrer les différents points cuspidaux. Si le point C2 est "évident" vous aurez un peu plus de mal à identifier les points C3 et C4 comme des points cuspidaux. Ils sont pourtant présents en bout d'une ligne d'auto-intesection. Au dessus du point C3 se trouve simplement ce que j'ai appelé un "posicoin", un point de concentration de courbure positive (un point de concentration de courbure négative est un "négacoin"). En déformant un poil cet objet on tombe sur une forme polyédrique de la surface Romaine de Steiner ( surface du 4° degrés inventée par Steiner à Rome. Voir sa présentation en réalité virtuelle).
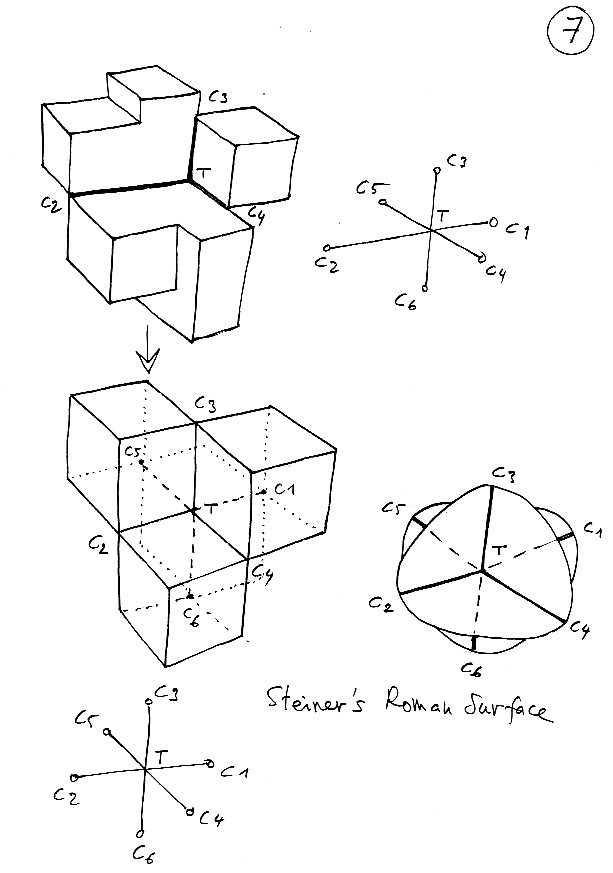
Donc, le tour est joué. Il existe différents types de surfaces, selon les règles que l'on s'impose. Les surfaces qui ne se recoupent pas elles-mêmes sont dites des plongements ( de la sphère, du tore dans R3). Quand elles se recoupent mais que le plan tangent varie continument on les appelle des immersions. Exemple : la bouteille de Klein dans sa représentation classique. Il nexiste pas dans R3 de représentation de la bouteille de Klein sous forme de plongement. Elle se recoupe nécessairement elle-même. Les immersions possèdent des ensembles d'auto-intersection exemptes de points cuspidaux. Ces courbes sont continues mais peuvent se croiser à où se trouvent des points doubles ou triples. Remarque : la sphère peut se présenter sous forme d'une immersion, en la faisant simplement se recouper elle-même. C'est d'ailleurs comme ça qu'on parvient à la retourner (A.Phillips, 1967, avec comme étape centrale le revêtement à deux feuillets d'une surface de Boy; B.Morin et J.P.Petit, 1979 avec comme modèle central le modèle à quatre oreilles de Morin, dont voici ci-après une représentation polyédrique que j'ai inventée il y a une dizaine d'années.
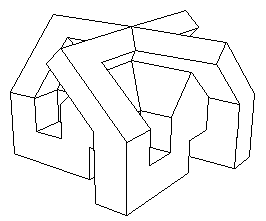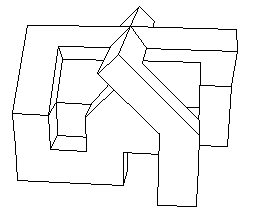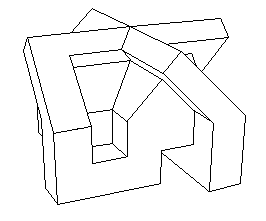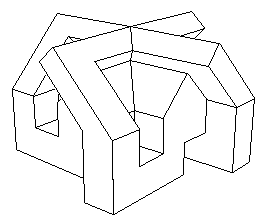
Plan pour montage de cet objet à l'aude d'un découpage
Si on étend la règle du jeu en supposant que ces objets possèdent des points cuspidaux on obtient des submersions (la Cross Cap, la Surface Romaine de Steiner). je ne sais pas si c'est le mot exact, mais comme je n'au trouvé aucun matheux qui puisse m'éclairer j'ai trouvé amusant d'en inventer un, provisoirement, jusqu'à ce qu'un géomètre-expert ne se manifeste. Ainsi la Cross Cap et la Surface Romaine de Steiner seraient des submersions du "plan projectif".
Pour tout vous dire, après mes déboires en matière de MHD sur vingt-cinq années j'avais entamé ces travaux parce qu'ils me semblaient aussi éloignés que possible de toute application militaire. Mais, comme le faisait remarqué mon vieil ami Mihn, le terme submersion pourrait préter à confusion et laisser sous-entendre à la Marine Nationale qu'à travers ces recherches je tenterais de cacher quelque percée en matière de propulsion sous-marine.
La règle de "création-décréation" de paires de points cuspidaux permet de passer d'une submersion d'un objet à une autre et c'est ce que nous venons de faire en montrant que la Cross Cap et la Surface Romaine de Steiner étaient deux submersion d'un même objet appelé plan projectif. Ne cherchez pas à quoi ressemble un "plan projectif". Cet objet ne peut s'appréhender qu'à travers ses différentes représentations. Quant au mot plan projectif ça n'est qu'un parmi mille autres inventé par les mathématiciens pour égarer ceux qui voudraient pénétrer dans leur cercle fermé. Le Larousse ne vous sera d'aucune utilité en mathématiques.
Il nous reste alors à passer à la surface de Boy, qui est une immersion du plan projectif
Retour au sommaire " Transformation d'une Cross Cap en Boy "
Retour vers Nouveautés Retour vers Guide Retour vers Page d'Accueil
Nombre de consultations depuis le 25 octobre 2003 :