Italiano : Andrea Sambusetti, università di Roma

Cliccate qui per far comparire il disegno del modello in scala 1:1, da stampare e ritagliare.
Fotocopiandone quattro esemplari su cartoncino bristol di due colori
differenti, potrete costruire il modello voi stessi,
seguendo le indicazioni per montarlo

Avete senz'altro visto un oggetto bizarro ruotare instancabilmente sulla parte sinistra della pagina iniziale di questo sito. Di cosa si tratta?

Un giorno, quando troverò il tempo, installerò su questo sito una descrizione del rovesciamento della sfera, così come l'avevo illustrata nel numero di Pour la Science del gennaio 1979, cioé... 22 anni fa! Tutto ciò necessiterà di molti dettagli e di un'introduzione. Cosa vuol dire "rovesciare una sfera"? Una sfera non ha lo stesso significato per l'uomo comune e per il matematico-geometra. Per l'uomo comune, non è altro che il luogo dei punti dello spazio situati a una distanza R da un punto O prefissato. Un geometra continuerà a chiamare "sfera", invece, anche un oggetto che corrisponde a una "sfera deformata", come una patata per esempio. Per capire con maggiore precisione questi concetti, procuratevi il CD di Lanturlu contenente il fumetto "Topologicon". Ma il matematico va anche un po' più lontano. Una superficie è detta "regolare" quando in ciascuno dei suoi punti si può definire un piano tangente. Ciò permette già di pensare ad un'infinità di deformazioni regolari possibili della sfera, nelle infinite possibili forme di una patata, variando inoltre in modo arbitrario l'area di tale superficie. Ciò detto, nel nostro universo fisico una persona che tenti di rovesciare la sfera (portarne cioè la superficie interna all'esterno) si troverà di fronte all'impossibilità di riuscire a far auto-attraversare la sua superficie. Quando si assume questa ipotesi, ovvero si proibisce che la superficie si autoattraversi o anche solo che si "tocchi", il matematico parla di embedding della sfera S2. Ma un matematico si permette sempre tutto. Una sfera è, per lui, un oggetto "virtuale" e non materiale, in cui l'attraversamento di una falda è considerato possibile. La successione di disegni qui sotto mostra una sfera che si autoattraversa. Una rappresentazione del genere, che ammetta cioè degli autoattraversamenti, è detta un' immersione.

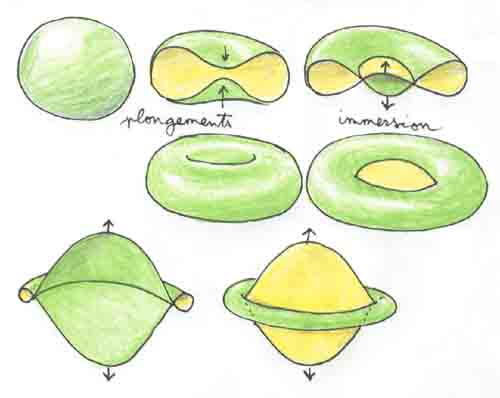
Un'immersione possiede pertanto un insieme di auto-intersezione (qui si tratta di una semplice curva circolare). Il piano tangente, però, deve variare in maniera continua. Ciò premesso, quando si guarda il disegno sopra, si vede bene che l'operazione porta una parte della superficie interna (rappresentata in verde) all'esterno. Per completare il rovesciamento, bisognerebbe schiacciare questa specie di budello equatoriale. Qui sembra esserci un problema: questo schiacciamento distruggerebbe la continuità del piano tangente, e tale trasformazione conterrebbe quindi un passo che non è un'immersione.

Un giorno un matematico americano, Stephen Smale, dimostrò che "la sfera S2 possiede una sola classe di immersioni". Questa frase sibillina aveva come corollario il fatto che si sarebbe dovuti poter passare, tramite una trasformazione che contenga solo vere immersioni, dalla sfera "standard" alla sua rappresentazione "antipodale", cioè in cui ogni punto è scambiato con il suo antipodale: in parole povere... una sfera rovesciata. Raoul Bott era il capo di Smale. Tanto la dimostrazione formale di questo fatto sembrava corretta, tanto nessuno sembrava capace di realizzare concretamente questa operazione di rovesciamento. Bott continuava a chiedere a Smale "mi faccia vedere come penserebbe di procedere"; al che, Smale, notoriamente senza peli sulla lingua, rispondeva "non ne ho la più pallida idea". Smale ottenne in seguito la medaglia Field, l'equivalente del Nobel per la matematica. Per inciso, vi domanderete forse perché non esista il premio Nobel per la matematica. La risposta è semplice: sua moglie è scappata con un matematico.

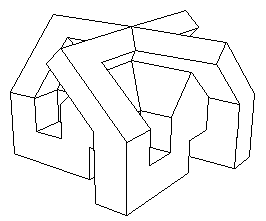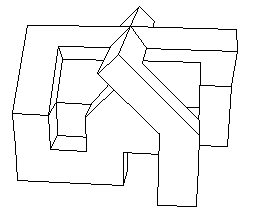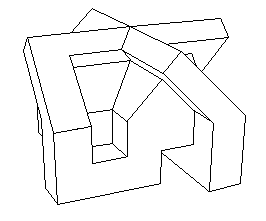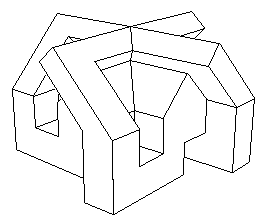
Le cose restarono così per un bel po' di anni, finché un matematico americano di nome Anthony Phillips pubblicò nel 1967, su Scientific American, una prima versione di questo rovesciamento, estremamente complicata. La seconda fu inventata agli inizi degli anni settanta dal matematico francese (non vedente) Bernard Morin. Fui il primo a disegnare la successione delle trasformazioni, che sarà oggetto, come vi ho annunciato, di un prossimo articolo su questo sito, peraltro ben abbondante. Comunque, tutto ciò ci porta ad una considerazione. Le superfici possono essere rappresentate in forma poliedrica. Un cubo o un tetraedro possono essere considerati delle rappresentazioni poliedriche della sfera, nel senso che questi oggetti hanno la stessa topologia. Su questo punto, consultate il mio Topologicon. Inoltre si capisce che, se è possibile rovesciare la sfera, sarà ugualmente possibile rovesciare un cubo. La trasformazione inventata da Bernard Morin (che ho illustrato nell'articolo del gennaio 1979 su Pour la Science) passa per un modello centrale. Esiste una simmetria in questa successione. E' quella che chiamo "modello centrale a 4 orecchie". Sto anticipando delle cose. Comunque, come la sfera si presta a rappresentazioni poliedriche, altrettanto vale per i passi successivi di questa trasformazione. Quello che vedete ruotare nella mia pagina iniziale è la versione poliedrica del modello centrale del rovesciamento della sfera, che ho inventato una decina di anni fa. L'interesse di tali modelli poliedrici sta nel fatto che si possono costruire con delle superfici piane. Si possono anche costruire con carta e forbici. Date un'occhiata al disegno qui di seguito (ringrazio tra prentesi il mio amico Christophe Tardy, che ha prodotto gli elementi della misura giusta).

Grande

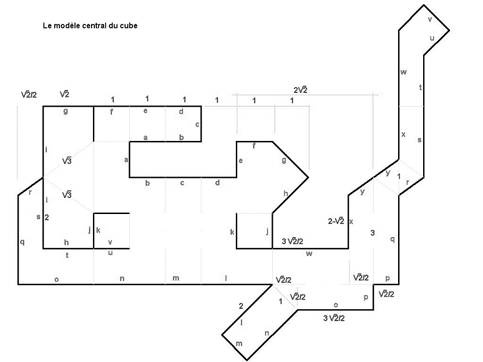
E' un piano di montaggio di cui avete qui una vista generale. Ma per stamparlo è preferibile che passiate alla pagina découpage. Stampatela. Dopodiché, muniti di questo esemplare stampato sulla usuale carta della vostra stampante, fotocopiatene 4 copie identiche, due su cartoncino bristol verde, e due in giallo. Sarete in grado, per mezzo di questi fogli da ritagliare, di costruire il modello centrale del rovesciamento del cubo.

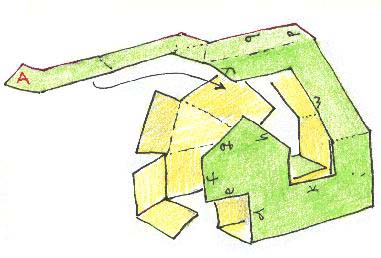
Sugli elementi da ritagliare ci sono coppie di lettere : a , b c , d , e , f ecc.... E' sufficiente di piegare il foglio portando a coincidere le stesse lettere, e poi fissare le faccie con del nastro adesivo trasparente. I disegni che segono mostrano la maniera di montare uno dei quattro pezzi. Ecco innanzitutto come bisogna iniziare a piegare uno dei quattro elementi :

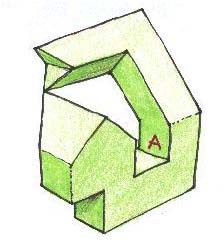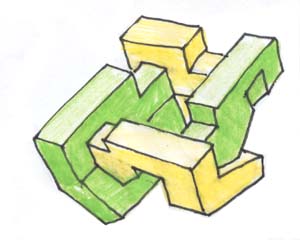
Ecco due dei quattro elementi, visti da angoli differenti.

Si sistemano quindi in modo da dar luogo ad un oggetto con una simmetria di ordine quattro, in ci si alternano elementi verdi e gialli. Per vederlo in 3d, gettate uno sguardo alla realizzazione di Tardy, alla sezione "realtà virtuale". Il modello centrale è montato e anche realizzato in "vrml" in questa sezione. Eccolo riprodotto da vari punti di vista :

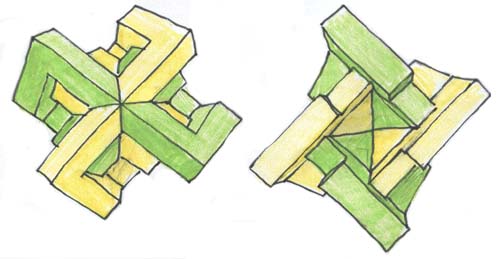
Non si può dire che un punto di vista corrisponda al "sopra" e l'altro al "sotto", dal momento che queste denominazioni sono perfettamente arbitrarie. Nell'immagine di sinistra, il punto "centrale" corrisponde al "punto doppio" (in cui due falde si incrociano) del modello centrale di Morin, mentre il punto centrale dell'immagine a destra corrisponde al "punto quadruplo" dello stesso modello (in cui quattro falde si incrociano). Ho dovuto orientare l'oggetto con molta attenzione, in modo che la figura di sinistra non evochi una svastica. A parte ciò, dal punto di vista architetturale, questa rappresentazione poliedrica del modello centrale di Morin avrebbe potuto costituire un bel progetto di Casa della Cultura Nazionale Socialista.

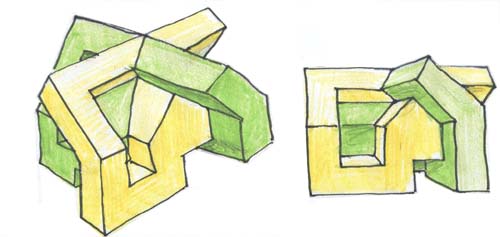
Un'ultima osservazione : non esiste una buona rappresentazione poliedrica del rovesciamento della sfera (ovvero del cubo). Per "buona" intendo una successione di modelli abbastanza espliciti che possano essere descritti sotto forma di fogli da ritagliare in modo relativamente facile, come il modello sopra. Ci sarebbe da fare uno studio in questa direzione, alla portata di chiunque, anche un non-matematico, per esempio uno scultore. Più di vent'anni fa ero insegnante di scultura alla Ecole des Beaux-Arts di Aix en Provence, al tempo in cui era direttore il mio caro amico Jacques Boullier. E' in quei locali che nacque la prima rappresentazione meridiana dell asuperficie di Boy tramite ellissi, chiave della costruzione della prima equazione implicita data da Apéry. Devo dire che già all'epoca fui sorpreso dall'immaginazione geometrica degli studenti d'arte, che superava spesso quella dei... geometri.

Contatore installato il 31 dicembre 2001. Numero di connessioni :

      Torna alla pagina Novità          Pagina iniziale