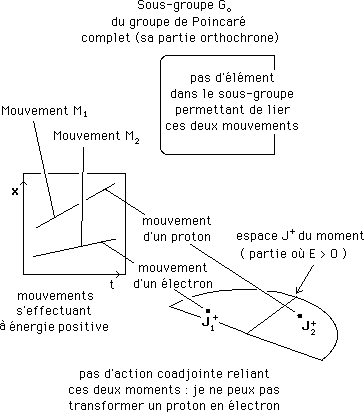
On a vu plus haut que le groupe de Poincaré complet avait contracté une maladie liée à sa proche parenté avec un groupe à quatre composantes, le groupe de Lorentz. Il est ainsi composé de deux ensembles, le sous-groupe orthochrone Go et l'ensemble antichrone Gat ( qui n'est pas un groupe à lui seul ). Voilà donc le terrain de jeu complet :

(208)

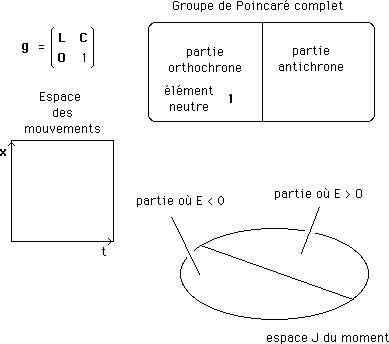
Dans l'espace J des moments des moments correspondant à des mouvements s'effectuant dans l'espace des mouvements avec des énergies négatives :

(209)

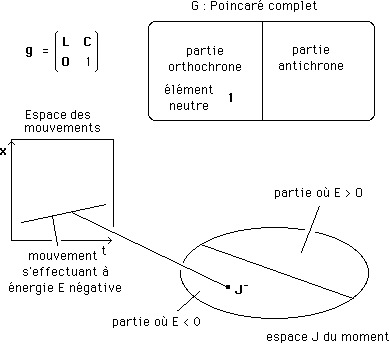
Ce sont ces mouvements-là qui ennuient fort les physiciens. En cas de rencontre entre deux particules, dans le même espace, l'une à énergie positive et l'autre à énergie négative. Résultat : du RIEN.

 
Avant de nous poser des problèmes aussi épineux, est-ce qu'on ne pourrait pas se concentrer sur les particules "normales" au sens de Coluche ?

D'accord. Faisons comme Souriau :

- Amputons le groupe de sa partie antichrone et ne gardons que le sous-groupe orthochrone.
- Amputons l'espace des moments de cette partie se référant aux points matériels à énergie et masse négatives.

(210)

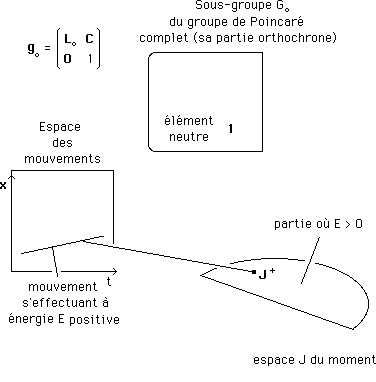
Terrain de jeu restreint, mais alors : plus de problème.

J + est censé figurer un moment lié à un mouvement s'effectuant à énergie positive.

Inversement J - figurera un moment lié à un mouvement s'effectuant avec une énergie E < 0 .

 
Je choisis un élément g dans mon sous-groupe orthochrone Go. Il provoque un changement de mouvement. Le point figuratif saute, dans l'espace des moments. Mais c'est toujours sans problème.

(211)

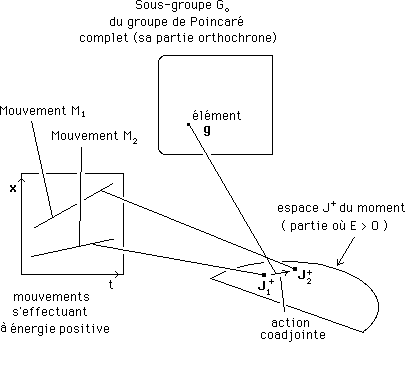
A gauche j'ai par exemple deux mouvements différents d'une même particule.

Les espèces de particules sont des "espèces de moments". Dans cet espace des moment J je peux distinguer des domaines, correspondant aux différentes espèces. Ci-après on s'est limité à deux espèces de particules, ce qui correspond à cette frontière linéaire, coupant le demi-disque en deux. :

(212)

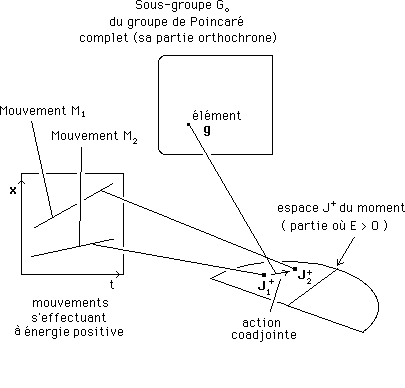
Les points figuratifs, dans le sous-espace J+ du moment, attaché aux mouvements qui s'effectuent avec des énergies positives, j'ai mis deux points correspondant à une même espèce. Il s'agit par exemple de deux mouvements, par exemple de l'espèce électron.

J'ai fait figurer une flèche ( action coadjointe) qui permet de passer en continu d'un de ces mouvements à l'autre.

Par contre, si mes points étaient choisis dans le sous espace des moments , dans des régions correspondant à deux espèces différentes ( par exemple électrons et protons ) il n'y aurait pas d'élément du groupe, donc d'action coadjointe permettant de passer d'un de ces mouvements à l'autre. Ce qui a été évoqué plus haut.

(213)