Retour sur la question du moment.

 
Nous sommes prêts à nous lancer dans une aventure, c'est à dire à écrire une simple matrice, à inventer un groupe dépendant d'un certain nombre de paramètres et susceptible d'agit sur un espace possédant un certain nombre de dimension (ici, en l'occurrence, dix). Puis, œuvrant à la manière de boustrophédons (de bous, le boeuf et strophedein, le sillon) nous avons calculé cette fameuse action coadjointe du groupe sur son espace des moment et défini celui-ci, ses attributs, des composantes, et la manière donc cette action coadjointe agit sur celles-ci, ce à quoi nous tenterons alors de donner un sens , une interprétation physique .

Revenons un instant sur le chemin parcouru en remettant sur le métier un groupe qui, s'il semble formellement plus compliqué :

(168)

 
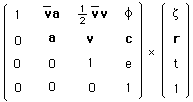
nous a fourni une action coadjointe, ci-après :

(169)

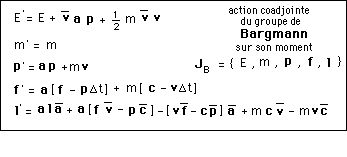
laquelle a fait aussitôt apparaître les composantes de cet objet ponctuel , de ce point matériel .

(170)
 

De toute façon, nous savions au départ que ce mystérieux moment devrait être composé de onze scalaires, puisque leurs nombre devait être égale à la dimension du group, qui est également onze. Coup d'oeil à la matrice-éléments du groupe de Bargmann :

(171)

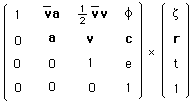
a est une matrice "orthogonale", une matrice "qui fait tourner"ou qui "est liée à une rotation dans un espace 3d". Nous l'avions explicitée dans le cas de deux dimensions. Auquel cas cette matrice ne dépendait que d'un seule paramètre, l'angle de rotation a .

En 3d elle va dépendre de trois paramètres, les angles d'Euler :
 

Le vecteur vitesse v donne trois paramètres supplémentaires :
 

La translation spatiale c en introduit trois autres :
 

et la translation temporelle un de plus :

Total : dix.

 
Ajouter un mystérieux onzième paramètre : f " lié au monde quantique". Bon....

Total général : onze. Donc un moment à onze composantes, que je pourrais mettre sous la forme :

(172)

Calculant à tout vat, j'ai pu mettre en évidence des liens entre ces composantes du moment, la façon dont elle s'articulaient entre elles, se regroupaient pour se constituer :

- en scalaires ( E et m )
- en vecteurs ( p et f )
- en matrice : l .

 
C'est comme si je disais : un être humain à une tête, deux bras et deux jambes. Mais comment se déplace-t-il, comment ces "composants" sont-ils "articulés" entre eux ?

 
L'action coadjointe nous a ensuite précisé comment le groupe agissait sur ces éléments du moment :

(173)

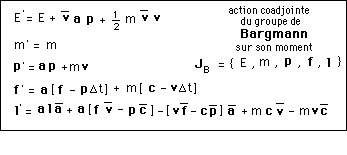
Dans ce tableau, on a tout de suite vu que dans ce fameux moment il existait une de ses composantes, m (à laquelle on aurait tout aussi bien pu laisser son nom initial, arbitraire : J₂), un simple scalaire, qui restait insensible à cette action du groupe.

 
Nous avons alors pensé que ce statut conviendrait assez bien à ce que nous croyons savoir de la masse m dans un monde non-relativiste.
 

Ces formules du moment nous fournissait les valeurs de ces apparences nommées attributs, composantes du moment associé au point matériel : nous traquons la matière dans son ses états : quand elle est est tournée (a) , déplacé spatialement (c), temporellement (e), animée d'une vitesse v et mystérieusement déplacée dans cette toute aussi mystérieuse cinquième dimension z , d'une quantité f , dont on nous dit que "tout ceci est lié au quantique".

Bon....

 
Le moment subit une transformation, via l'action coadjointe qui agit dessus. Il passe d'un "état" :

(174)

 
à un autre "état :

(175)

 
Pourquoi ne pas considérer alors une espèce "d'état fondamental", qui serait :

(176)

 
en disant qu'une action coadjointe ferait alors apparaître des attributs que je pourrais reconnaître.

Mais je vois qu'il me faudrait au moins mettre la masse m, puisque l'action coadjointe ne la change pas. Ainsi, si je la prenais nulle, elle le resterait. Donc je dois partir de l'objet de base :

(177)
 

 
Cet objet n'a pas d'énergie . C'est l'action du groupe qui lui en confère une. De même qu'elle lui confère une impulsion, un passage et un tournoiement.

Une énergie cinétique :

(178)
 

Une impulsion (le physicien intégriste dirait une "quantité de mouvement" ) :

(179)

 
Un "tournoiement", une sorte de "moment cinétique propre", comme si notre point matériel pouvait tourner sur lui-même (ce qui pourrait être le cas pour une petite bille de métal, de masse m, assez petite pour pouvoir être assimilée à une chose ponctuelle) :

(180)
 

Il reste cet objet éminemment déconcertant pour un physicien, le "passage". E agissant sur mon point matériel, je lui ai conféré un "attribut-passage", alors qu'au départ il n'en avait point, et celui-ci se trouve être :

(181)
 

Les composante de la matrice groupe ont toutes été traitées comme des grandeurs indépendantes. C'est "le transport le plus général".

Finalement, quand on agit sur un être humain, celui-ci peut se trouver "transporté" et "mis dans tous ses états".

Ici il s'agirait du transport le plus général, où notre point matériel est,
soit :