

 |
14
|
Extension centrale du groupe de Poincaré.
On trouvera mention d'une telle extension dans le livre de J.M.Souriau, sutructure des Systèmes Dynamiques. Sa méthode de quantification géométrique lui permet, à partir de groupe, de retrouver les équations de la Mécanique Quantique. Par exemple le groupe de Bargmann, décrivant le point matériel non relativiste, conduit à l'équation de Schrödinger, également non relativiste.
Le point de départ est le groupe de Galilée. Il s'agit d'une matrice de format (5,5) construite de cette façon :
(152)
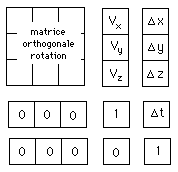
La matrice de rotation dépend de trois paramètres, les angles d'Euler. Donc la dimension du groupe est dix.
En utilisant les notations :
(153)
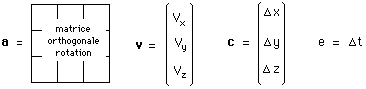
(154)
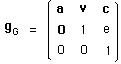
associé à l'espace-temps :
(155)
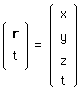
Aussi étrange que cela puisse paraître, la construction de l'action coadjointe du groupe sur son espace des moments ne fait pas apparaître la masse m, en tant qu'objet géométrique. Cela ne peut se faire qu'à travers une extension non-triviale de ce groupe, le groupe de Bargmann ( 1960).
(156)
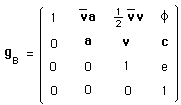
La présence du scalaire f donne à ce groupe une dimension de plus : onze.
Ce groupe agit sur un espace à cinq dimensions, l'espace-temps, plus une dimensions additionnelle z , à travers l'action :
(157)
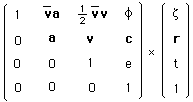
L'action coadjointe du groupe de Bargmann sur son moment a été donnée plus haut. On voit que l'adjonction du scalaire f , en ajoutant une dimension au groupe, ajoute une composante au moment, qui s'identifiera alors avec la masse m ( laquelle est au passage conservée : m' = m).
Partant du groupe de Bargmann, et utilisant sa méthode de quantification géométrique, Souriau peut alors construire l'équations de Schrödinger, non-relativiste.
L'équation quantique relativiste est l'équation de Klein-Gordon. Il était alors logique de chercher de quel groupe elle pouvait dériver. C'est l'extension centrale :
(158)
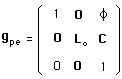
"pe" pour "Poincaré étendu". On a ici construit le groupe de Poincaré à partir du sous-groupe orthochrone du groupe de Lorentz Lo .
L'espace associé à ce groupe est également un espace à cinq dimensions :
(159)
Cette extension est plus simple que celle de Bargmann, mais en fait les choses sont toujours plus aisé en relativiste. On démontre, accessoirement, qu'entre le 1 et le f de la première ligne ne peut se trouver que la matrice ligne 0 = ( 0 0 0) : que des zéros.
La méthode de quantification géométrique conduit alors à l'équation de Klein-Gordon. S'agissant de l'action du groupe sur son espace des moments on obtient ceci :
(160)
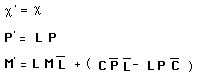
Le calcul n'est pas compliqué. Il se calque en fait complètement sur le calcul de l'action coadjointe du groupe de Poincaré sur on moment.
On calcule l'anti-action :
(160 b )
puis on exprime l'invariance du produit scalaire ( dualité ) :
(160 c)
Si vous vous sortez de ce calcul, ça sera franchement bon signe. Cela signifiera que vous commencez à entrer dans ce bazar.
Apparaît donc un scalaire c , dont la seule fonction est de se conserver. Que signifie-t-il ? Pas d'explication. C'est simplement "quelque chose qui se conserve". On peut lui attribuer par exemple le statut de charge électrique.
La première idée qui vient est de réaliser ce type d'extension plusieurs fois :
(161)
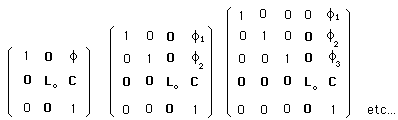
On montrera plus loin qu'on peut ainsi réaliser cette opération indéfiniment et que ceci ajoute à chaque fois un scalaire supplémentaire :
(162)
avec comme action coadjointe :
(163)
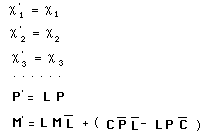
On considérera alors que certaines valeurs discrètes des composantes du moment figurent les charges de la particule.
Bon, dira le lecteur, effectivement, on pourrait ajouter par exemple six lignes supplémentaires. On obtiendrait alors l'invariance de scalaires qu'on pourrait identifier à :
(164)
(165)
(166)
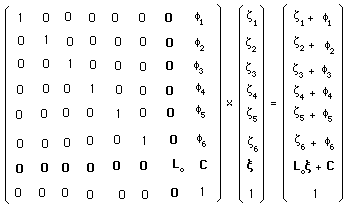
Encore une fois on construit le groupe autour du sous-groupe orthochrone Lo du groupe de Lorentz :
Lo = Ln (composante neutre) » Ln (inversion de l'espace).
Ce groupe, à deux composantes, fait alors simplement apparaître six scalaires qui accompagnent la particule sans interagir avec quoi que ce soit. Le moment devient :
(167)
Jp étant la "partie Poincaré". Mais cela reste d'un intérêt limité.
