A partir de groupe de Lorentz on fabrique le groupe de Poincaré, déjà évoqué :

(142)

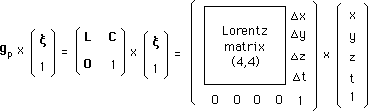
C est le vecteur "translation spatio-temporelle".

(143)

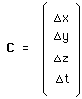
Ce groupe de Poincaré aura également quatre composantes, chacune liée à la composante correspondante du groupe de Lorentz.

Ci-dessus, l'action du groupe sur son espace des mouvements. Mais ce qui est intéressant, ce sont les actions des quatre composantes sur le moment . Voir :Souriau, Structure des Systèmes Dynamiques, Dunod 1973 (et Birkhauser 1997, en anglais), chapitre III, page 197, section intitulée: Inversions d'espace et de temps.

Rappelons les composantes du moment associé au groupe de Poincaré :

E : énergie
p : impulsion
f : passage
l : tournoiement

 
Pour être proche des notations de Souriau, appelons :
- Ln la composante neutre du groupe de Lorentz.
- Ls celle qui inverse l'espace.
- Lt celle qui inverse le temps
- Lst celle qui inverse les deux.
 

C étant une translation spatio-temporelle, les quatre composantes du groupe de Poincaré sont :

gp ( Ln , C) composante neutre
gp ( Ls , C) inversant l'espace
gp ( Lt , C) inversant le temps
gp ( Lst , C) inversant l'espace et le temps.

 
Cherchons les effets sur les composantes du moment . Nous devons considérons les formules donnant l'action du groupe sur son espace des moments :

(144)

 
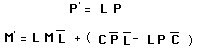
P est le quadrivecteur :

(145)

 
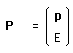
On peut écrire les matrices à analyser :

(146)

avec l = ± 1 et m = ± 1 .
Ln = L ( l = 1 ; m = 1)
Ls = L ( l = - 1 ; m = 1)
Lt = L ( l = 1 ; m = - 1)
Lst = L ( l = - 1 ; m = - 1)
 

(147)

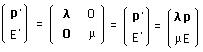
(148)

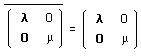
Passons à l'examen de l'action sur le tournoiement et le passage.

(149)

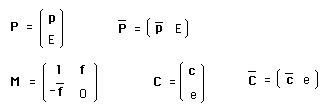
Mais, dans ce qui nous intéresse C = 0

(150)

d'où l' = l et f' = l m f

 On en déduit :

(151)

Les inversions ne changent jamais le tournoiement l .

 
Par contre, inversion temporelle et inversion de l'énergie , E ---> -E , sont synonymes.

 
Le tournoiement est synonyme de spin, lorsqu'il est quantifié. Aucune inversion de l'altère.

 Le spin (en tant que module du vecteur tournoiement de la particule) n'est qu'un nombre.

 
L'énergie d'une particule au repos est mc².

L'inversion temporelle est synonyme d'inversion de la masse m.

L'inversion spatiale n'inverse pas la masse.

Les deux premières composantes du groupe sont baptisées par Souriau orthochrones, et les deux dernières antichrones .

Il note que tout ceci soulève le problème des masses négatives, que n'aiment guère les physiciens. En effet, quid du résultat de la rencontre de deux particules dotées d'énergies

+ mc² et - mc²

Il y a annihilation complète . Il ne s'agit pas de la simple annihilation matière-antimatière, qui, elle, donne des photons. Il s'agirait d'un phénomène qui donnerait du rien à l'état pur.

 
Pour éviter cet écueil des masses négatives, Souriau envisage deux solutions. La première consiste à décider purement et simplement que les particules à masse négative n'existent pas. La seconde consiste à exclure les transformations antichrones.

Paraphrasant nous pourrions dire que :

- Dieu, dans son infinie sagesse...
 

Continuons à mettre en place des éléments qui serviront de point de départ à notre propre travail.