Il n'y a plus de lien direct entre énergie et impulsion, comme pour les photons et les neutrinos, particules à masse nulle.

(131)

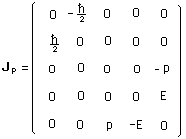
m étant la masse au repos, qui s'identifie alors avec la masse émergeant du groupe de Bargmann, on a :

(132a)

Limitons-nous à :

Proton
électron
neutron
et leurs antiparticules.

 
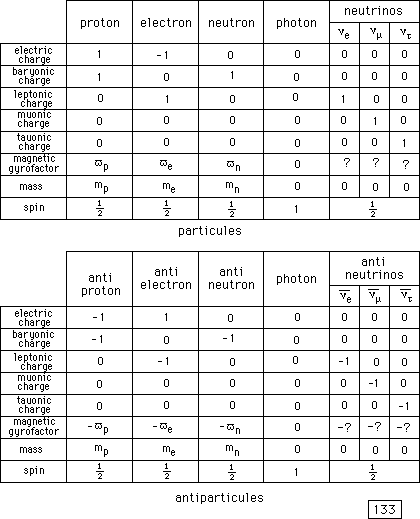
Les particules possèdent différentes charges, attributs, qui n'émergent pas non plus du groupe de Poincaré :

- La charge électrique e = ± 1
- La charge baryonique cB = ± 1
- La charge leptonique cL = ± 1
- La charge muonique cm = ± 1
- La charge tauonique ct = ± 1
- Le coefficient gyromagnétique v

L'inversion de toutes ces quantités correspond à la C-symétrie. On peut donc regrouper tout cela selon le tableau ci-après :

(133)

qui peut prendre une orientation quelconque, de même que le spin.

Le moment magnétique est égal au coefficient gyromagnétique v multiplié par le spin s.

(134)

Ici nous avons utilisé une lettre grasse s pour le spin. Ceci signifie que la direction du spin des particules peut être quelconque. Par contre leur module est une de leurs caractéristiques et est fondamentalement invariant ( quantification géométrique du tournoiement des particules).

La C-symétrie, la conjugaison des charges, inversant le coefficient gyromagnétique v ,inverse aussi le moment magnétique.

Aimants permanents.

Si on place un morceau de fer doux dans un champ magnétique assez puissant, puis qu'on réduise ce champ, le métal va conserver une aimantation permanente. Que s'est-il passé ?

Le champ magnétique aligne les spins des électrons, lesquels se comportent comme de mini-aimants, des petits dipôles magnétiques..

Mais pourquoi conservent-ils alors la direction qu'on leur a imposée ? Par mimétisme. Chaque électron s'aligne selon le champ magnétique créé par ses voisins. Et, les autres faisant de même, tous ces moments conservent leur parallélisme. C'est du "Panurge spatial". A moins qu'on ne chauffe le morceau de métal, ou qu'on cogne dessus, auquel cas on finira par déranger cette belle ordonnance électronique.

Moment magnétique de l'antimatière.

La conjugaison de charge, liée à la transformation matière-antimatière au sens de Dirac (on verra plus loin ce que cela signifie), entraîne l'inversion du moment magnétique, à cause de l'inversion du coefficient gyromagnétique, le spin restant inchangé.

Bien entendu cette C-symétrie ne modifie ni l'énergie, ni l'impulsion de la particule.

Les quatre composantes du groupe de Lorentz.

Comme on l'a vu, l'élément L du groupe de Lorentz L est défini axiomatiquement. Il doit obéir à :

(135)

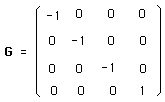
(136)

Toute matrice L obéissant à cette définition fait partie du groupe L. C'est une matrice de format (4,4), qui peut par exemple agir sur :

(137)

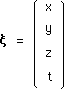
autrement dit sur l'espace-temps. On est alors en droit de se demander si ces matrices ne sont pas susceptibles d'opérer des symétries, dans cet espace. Est-ce qu'on ne pourrait pas, par exemple, changer x en - x ? Est-ce que les matrices ne pourraient pas être classées en différents sous-ensembles, celles qui opéreraient ceci et celles qui ne réaliseraient pas l'opération.

Il y a belles lurettes, ( en anglais many beautiful candles ago), on a exploré tout cela, et montré que le groupe de Lorentz était constitué en fait de quatre types de matrices.

Ln- Celles qui n'inversaient ni l'espace, ni le temps.
Ls - Celle qui inversaient l'espace
Lt - Celles qui inversaient le temps
Lst - Celles qui inversaient les deux.

On appelle ces ensembles des composantes d'un groupe. Le groupe de Lorentz est donc un groupe comportant quatre composantes.

Nous pouvons tout de suite produire quatre matrices dont chacune appartient au sous-ensemble cité :

(138)

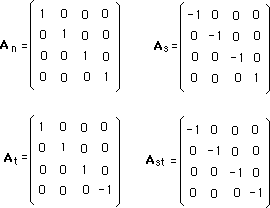
An = 1 ( élément neutre), appartient à Œ Ln : n'inverse ni l'espace ni le temps.
As Œ appartient à Ls : inverse l'espace
At appartient à Œ Lt : inverse le temps
Ast Œ appartient à Lst : inverse à la fois l'espace et le temps.

 
Pour constituer un groupe ( en l'occurrence un sous-groupe du groupe de Lorentz) il faut qu'un ensemble de matrices contienne l'élément neutre 1 dans le format (n,n) considéré, ici : (4,4). Seules les matrices de l'ensemble Ln répondent à ce critère. Elles forment un sous-groupe du groupe de Lorentz . Comme cet ensemble de matrices contient l'élément neutre du groupe on l'appelle aussi la composante neutre du groupe . Les autres ensembles de matrices ne constituent pas des sous-groupes (impossible : elles ne contiennent pas l'élément neutre).
 
 

Remarque :

(139)

On peut alors considérer l'ensemble Lo = Ln » Ls qui est un sous-groupe du groupe de Lorentz et qu'on appelera orthochrone [1]. Les matrices Lac = Lt » Lst ne constituent pas un groupe, mais l'ensemble des composantes liées à l'inversion du temps, ensemble qu'on appelera antichrone [12]. Le groupe de Lorentz complet est :

(140)

Mais on peut aussi remarquer que l'élément :

(141)

couvre le groupe complet.