

 |
11
|
On s'aperçoit qu'on obtient alors deux types de photons :
(126)
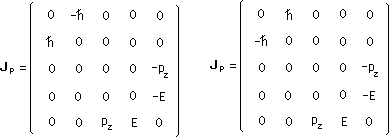
Un photon "droit" (polarisation droite) et un photon "gauche" (polarisation gauche), qui diffèrent par leur hélicité. Deux photons qui cheminent dans la même direction (OZ), à la vitesse c, et ont la même couleur (leur énergie E).
Pour un photon, l'énergie E et l'impulsion p ne sont par ailleurs pas indépendantes.
(127)
ce qui nous donne :
(128)
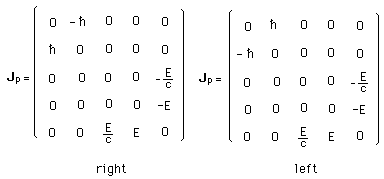
En dehors de ces caractéristiques (énergie, direction de propagation, hélicité) le photon n'en a point d'autre. Il ne possède aucune "charge", si on veut, "toutes ses charges sont toutes nulles", ce qui fait de lui l'identique de son anti-particule (plus zéro étant identique à moins zéro).
Les neutrinos.
Considérées comme des particules de masse
nulle (ce qu'ils sont, jusqu'à preuve du contraire) ils ont des matrices-moments
identiques à celles des photons, à cette différence près
que le spin est moitié :
(128b)
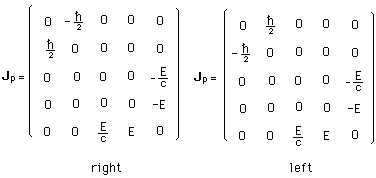
(129)
Les neutrinos, cheminant à la vitesse c, possèdent une impulsion -énergie, un spin, également quantifié, quoiqu'il soit différent de celui du photon. Le neutrino possède également une hélicité. Il y a des neutrinos à polarisation droite et des neutrinos à polarisation gauche.
Mais on sait qu'il existe en outre trois types différents de neutrinos, ce que le groupe de Poincaré ne fait pas apparaître et ne peut faire apparaître (il nous faudra le modifier dans ce qui suivra pour faire apparaître, géométriquement, le charges des différentes particules).
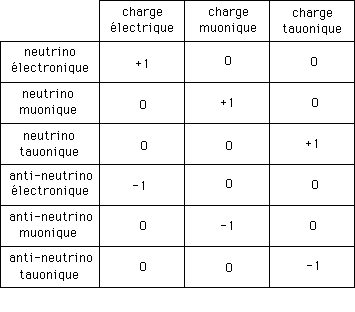
Ceci étant les neutrinos sont de trois types :
- électronique
- muonique
- tauonique
c'est à dire qu'on peut leur conférer trois types de charges :
e = électrique = +/-1 ( +/-; la "charge unitaire").
cm =
charge muonique = +/-1
cn =
charge tauonique = +/- 1
On appelle aussi cette inversion du signe des charges une conjugaison des charges ou une C-symétrie.
Les trois types de neutrinos doivent donc être associés aux anti-neutrinos correspondants :
(130)
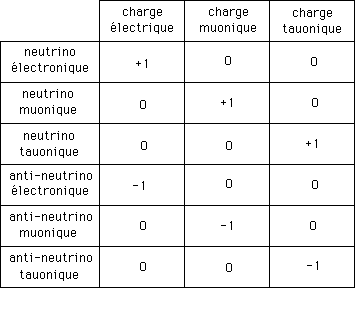
Mais cette distinction, à la fois sur les nombres
quantiques, les charges, et sur les dualité matière-anti-matière
n'est pas non plus inscrite a priori dans le groupe de Poincaré.
