

 |
10
|
Tout ce que je peux dire c'est :
- qu'en m'éloignant de la "cible" d'une distance c.
- en l'observant en me déplaçant moi-même
à une vitesse v.
- en étant, par rapport à cette cible, décalé
d'un laps de temps Dt
Par rapport à moi :
--- Je n'ai pas fait varier sa masse m.
--- Je l'ai dotée d'une impulsion m v ( quantité
de mouvement).
---- Je l'ai dotée d'un passage m [ c - v
Dt ]
---- et d'un tournoiement : ![]()
Explicitons celui-ci :
(118a)
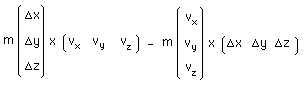
(118b)
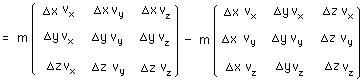
(118c)
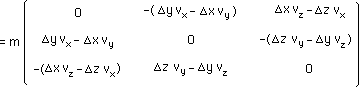
ou :
(118d)
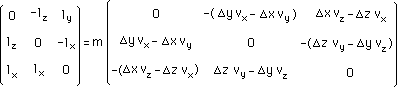
On peut considérer les trois composantes indépendantes de la matrice tournoiement l comme celles d'un vecteur. Celui-ci s'écrit alors :
(119)
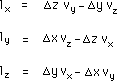
Bien qu'on n'ait pas défini le produit vectoriel dans notre espace, c'est à dire qu'on ne lui a pas conféré d'orientation droite-gauche, on peut considérer cela comme un produit vectoriel :
(120)
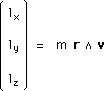
le v
à l'envers désignant le produit vectoriel. On voit que la dernière
ligne des formules donnant l'action coadjointe sur le moment correspond à
:
(121)
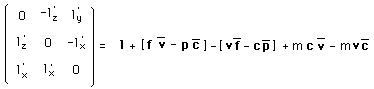
l étant une matrice et non un vecteur ( mais, dans nos notations, les lettres grasses désignent indifféremment les uns et les autres, le maigres se référant aux scalaires).
Ce vecteur produit vectoriel commence à ressembler,
pour le physicien, à quelque chose de connu : le moment cinétique
.
On prend une particule, on s'en éloigne de c et on l'observe en circulant à la vitesse v . Tout se passe comme si c'était l'inverse: que la particule soit éloignée d'un observateur supposé fixe et se déplace à une vitesse v .
(122)
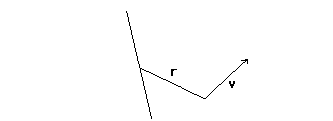
Reste le "passage" f = m [ c - v Dt
]
Il s'annule en faisant simplement c = v D t , c'est à dire en reliant la vitesse v et la translation spatio-temporelle :
(123)
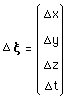
Reprenons l'expression du moment issu du groupe de Poincaré, exprimé dans un système de coordonnées où le passage soit nul :
(124)
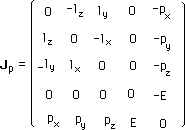
Une particule, c'est un choix particulier effectué dans le moment. Ceci étant, des changements de coordonnées permettent de faire disparaître le passage f et de ramener les composantes du tournoiement l et de l'impulsion P à une seule composante (mouvement en z) :
(125)
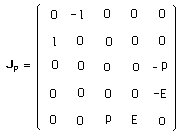
L'objet décrit par le groupe de Poincaré possède donc a priori :
- Une énergie E
- Une impulsion P
- Un tournoiement propre l
Le tournoiement c'est une masse, multipliée par une longueur, le tout multiplié par une vitesse. Ca a donc la dimension M L2 T-1 de la constante de Planck h.
La méthode de quantification géométrique
, développée par Souriau (voir Structure des Système Dynamiques,
Dunod 1973) permet de montrer que ce tournoiement doit être proportionnel
à :
(125b)
par valeurs demi-entières. C'est à dire soit l'unité (photon), soit 1/2 pour les autres particules comme l'électron, le proton, le neutron, les neutrinos, et leurs antiparticules.
