Le groupe de Poincaré décrit le mouvement relativiste d'un objet ponctuel. Semblablement, le groupe de Bargmann, dont l'expression sera donnée plus loin, décrit le mouvement non-relativiste d'un objet ponctuel, qu'on appelle alors "point-masse".

On voit donc que cette technique, le calcul de l'action coadjointe du groupe sur on espace des moments, a permis de faire émerger des éléments caché, des attributs de l'objet : les composantes du moment .

Ce qui est remarquable c'est que cette démarche, due à Souriau, fait apparaître les objets clefs du physicien en tant qu'objets purement géométriques . Il a donc réalisé là un travail sans précédent de géométrisation de la physique .
 

En dehors de l'énergie et de l'impulsion, des autres composantes, le "tournoiement" et le "passage" déconcertent passablement le physicien. Quès aco ?

L'expression des composantes du moment dépend évidemment du système de coordonnées choisi.

Le plus simple est sans doute de faire un bref retour au non-relativiste, autrement à l'expression de l'action coadjointe, telle qu'elle aurait émergé de l'analyse du groupe de Bargmann.

(111)

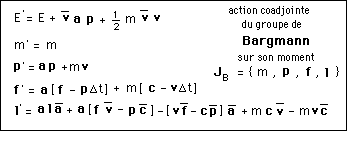
Formule mystérieuse. A quoi cela sert-il ? Comment cela fonctionne-t-il ?

Dans cet encadré ci-dessus le physicien aura reconnu quelques objets familiers :

(112)

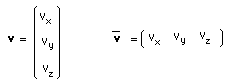
ne sont que deux expressions du vecteur vitesse { vx , vy , vz } la première sous forme d'une matrice colonne et la seconde sous la forme d'une matrice-ligne. Le produit des deux matrices est un scalaire :

(113)

quelque chose qui commence à ressembler à une énergie cinétique.

m v c'est une impulsion.

Le physicien traditionnel, s'agissant de la dynamique d'un point matériel, ne connait que trois choses :

- La masse m
- L'impulsion m v
- L'énergie cinétique 1/2 mv2

Oui, mais vitesse par rapport à quoi ?

 
Un groupe, c'est aussi un regard sur les choses. On peut alors soit considérer qu'on transporte, à l'aide du groupe, des objets (comme on l'a vu avec le groupe d'Euclide), vis à vis d'un observateur supposé fixe, soit, l'objet étant fixe, qu'on l'observe autrement.

Si on retient ce déplacement, ce transport des objets, s'agissant des groupes dynamiques , ceux de la physique (par opposition au groupe d'Euclide où le temps n'apparaît pas) on devra dire aussi qu'on anime les objets, en leur conférant vitesse v et énergie E .

 
Si on adopte le point de vue inverse : considérer que l'objet est fixe et envisager de se déplacer, soi,quel sens donner aux groupes ?

Le groupe d'Euclide signifierait alors :

"Vu d'ailleurs et sous un autre angle".

"L'ailleurs" c'est le vecteur translation :

(114)

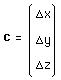
Le "vu sous un autre angle" c'est la matrice de rotation a, une rotation dans l'espace (que l'on pourrait expliciter avec les angles d'Euler, ce que nous ne ferons pas).

 
S'agissant de groupes dynamiques, ce regard, ce point de vue sur les "choses" doit être enrichi. Restant dans le contexte du groupe de Bargmann, le fait d'introduire cette vitesse v signifie qu'en plus, l'observateur, qui observe ce point-masse d'ailleurs (vecteur-translation c), sous un autre angle (matrice de rotation a), est aussi animé, par rapport à ce point masse supposé immobile, d'une vitesse v.

Et, pour être complet, pour corser le tout, il n'évolue pas dans le même temps que la particule, le point masse observé. Il est décalé par rapport à lui d'un laps de temps Dt. Autrement dit;  il l'observe d'ailleurs, mais c'est un ailleurs spatio-temporel, correspondant au vecteur translation spatio-temporelle :

(115)

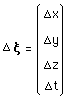
En ayant pris un tel "recul", par rapport à ce point-masse, qu'est-ce que je constate ? Primo que : m' = m

Cela n'affecte pas sa masse.
Je peux me simplifier la vie en annulant la rotation. C'est déjà assez compliqué d'observer un point masse d'ailleurs, vu d'un autre temps, décalé, juché sur un skate-board animé d'une vitesse v . Est-il en plus absolument indispensable de se tordre le cou ?

Non. Faisons a = 1.

mais on omet en général ce détail dans les calculs. L'action coadjointe, ainsi particularisée, devient :
(117)

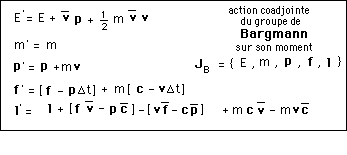
Considérer doit être pris ici dans son sens étymologique. Qu'est-ce que je fais quand je considère une situation, le ciel, un champ de bataille, le film pris par un avion-espion ?

Un huissier écrira :
- Considérant l'état des lieux.....

Vision statique, correspondant au groupe d'Euclide. L'huissier observe les objets à une distance c , au même moment (Dt = 0), en principe immobile ( v = 0). Les cas échéant sous un angle particulier, sous "un certain angle".
 

Un général, se promenant dans un avion de reconnaissance est une sorte d'huissier qui se déplace (v # 0).

 
Mais un chef d'Etat-Major qui visionne le film pris par un avion-espion, un "drone", est face à une situation décalée dans le temps. Il est obligé de se dire :
- Considérons la cible, vue depuis tel point, en virage incliné, à telle vitesse, et de plus telle qu'elle se présentait deux heures plus tôt...

La cible n'a pas de vitesse propre particulière. On ne saurait la considérer comme fixe, même si c'est "une installation fixe". Même la Terre se déplace, le Soleil aussi, la galaxie, etc.