

 |
8
|
(91)
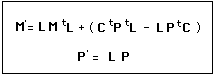
Cette action coadjointe peut s'écrire sous forme matricielle.
La matrice du groupe de Poincaré est :
(92)
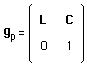
sa transposée est :
(93)
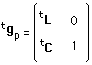
Considérons la matrice :
(94)
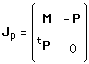
C'est à dire que nous allons mettre le moment
(95)
sous forme matricielle et formons le produit :
(96)
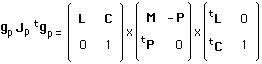
(97)
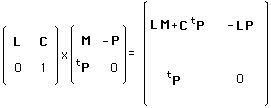
(98)
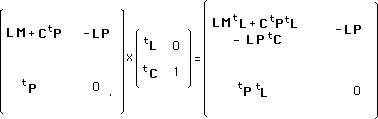
que je peux identifier à la matrice :
(99)
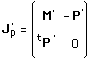
Jp est donc le moment du groupe de Poincaré, mis sous forme matricielle. Et l'action coadjointe s'écrit :
(100)
A titre d'exercice, le lecteur pourra, en s'appuyant sur les axiomes, vérifier que c'est bien une action .
Le moment du groupe de Poincaré peut être explicité comme suit :
(101)
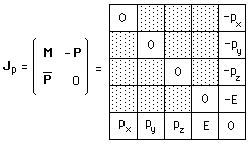
Cette matrice est antisymétrique ( ce qui entraîne que sa diagonale principale est constituée par des zéro). M est la matrice :
(102)
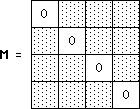
Explicitons-là :
(103)
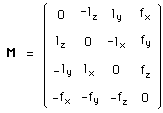
C'est bien une matrice antisymétrique, hypothèse formulée dès le départ, qui dépend de six paramètres :
(104)
Les trois derniers ( fx , fy , fz) sont les composantes d'un vecteur, le vecteur-passage f :
(105)
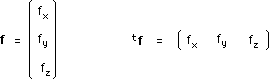
Les trois premiers ( lx , ly , lz) sont les composantes indépendantes d'une matrice antisymétrique (3,3), le tournoiement l :
(106)
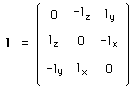
Ainsi :
(107)
Le vecteur P est le quadri-vecteur impulsion-Energie :
(108)
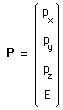
On peut alors expliciter le moment du groupe de Poincaré, dans toute sa généralité :
(109)
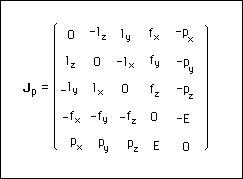
On vérifie que c'est bien un objet à dix composantes (nombre égal à celui des dimensions du groupe).
(110)
