Nous n'allons pas écrire les composantes du moment du groupe de Bargmann. Schématiquement écrivons le moment du groupe de Bargmann comme ci-après :

JB = { un scalaire m , plus les autres composantes du moment }

L'action coadjointe indique comment se transforment les différentes composantes du moment. Mais cette action coadjointe commence par la relation simple :

(63)

L'action coadjointe du groupe de Bargmann sur son moment commence par conserver conserve la masse, qui émerge ainsi avec un statut purement géométrique .

 
Construction de l'action coadjointe du groupe de Poincaré sur son espace des moments Jp.

Si vous êtes déjà complètement largué, laissez tomber. C'est normal et ça va devenir de plus en plus hard au fil des pages. Je ne sais plus trop, à ce stade, à qui s'adresse ce qui suit. A des physiciens théoriciens ou à des mathématiciens sans doute, mais probablement pas à des plombiers-zingueurs. Mais un élève de Grande Ecole ou de licence de physique, qui s'accrochera pourra suivre. Ce ne sont jamais que des matrices.

Tout part d'un groupe de matrices de format (4,4) qui constituent le groupe de Lorentz, dont l'élément est L.

Ceux-ci se définissent axiomatiquement à partir d'une matrice G :

(64)

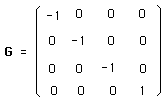
selon :

(65)

faisant intervenir la transposée de la matrice L.

Les matrice L forment un groupe.

Démonstration.

L'élément neutre est L = 1 :

Soient L₁ et L₂ deux élément de l'ensemble. Vérifions que le produit L₁L₂ appartient au groupe. Si c'est le cas :

Mais :

Donc :

^t( L₁L₂ ) G  L₁L₂ = ^tL₂ ^tL₁ G  L₁L₂ =  ^tL₂ ( ^tL₁ G  L₁) L₂ = ^tL₂G L₂

Calculons ensuite l'inverse de la matrice L . On part de la définition axiomatique des éléments L :

^tL G L =G

On multiplie à droite par L^-1 :

^tL G  L L^-1  =G  L^-1

^tL G = G  L^-1

On multiplie à gauche par G :

G  ^tL G =G  G  L^-1

G  ^tL G = L^-1

Donc la matrice inverse de L est :

Soit :

(66)

 
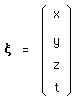
le vecteur espace-temps. La matrice G vient de la métrique de Minkowski, qui peut alors s'écrire ( avec c = 1) :

(67)
 

Exercice : montrer que la matrice inverse obéit à :

(68)

On introduit alors un vecteur translation spatio-temporelle :

(69)

 
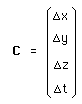
A partir duquel on fabrique l'élément gp du groupe de Poincaré :

(70)

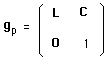
Exercice : montrer que ceci forme un groupe et calculer la matrice inverse :

(71)

 
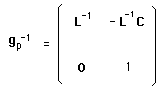
Ci-après le "vecteur tangent au groupe, élément de son "Algèbre-de-Lie" :

(72)

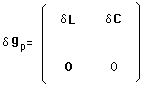
A partir de ceci on va calculer l'anti-action :

(73)

Par souci de commodité de calcul, on remarque que ;

(74)

 
est une matrice antisymétrique. Appelons-là :

(75)

donc :

(76)

Posons :

(77)

A partir de ce matériel on va constituer l'anti-action :

(78)

Tous calculs fait on obtiendra l'application :

(79)

 
Si vous voulez sauter cette partie de simple calcul matriciel, reportez vous équation (80) , bas de page

 (79a)

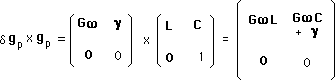
 (79b)

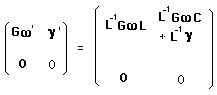
d'où les éléments de l'anti-action :

 (79c)

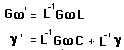
mais :

 (79d)

donc :
(79e)

mais GG = 1 donc :
(79f)

d'où on tire l'application :
(79g)

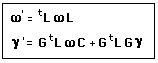
Ce qui constitue l'anti-action cherchée, l'application :

(80)

  Retour vers le sous-sommaire "groupes et physique"