Une matrice carrée de rang (n,n) agit sur un vecteur colonne (n,0). On a vu que le groupe d'Euclide 2d, se référant à un espace (x,y), ne mettait pas en jeu des actions sur des vecteurs-colonnes :

(51)

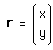
mais sur des vecteurs-colonnes :

(52)

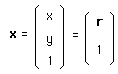
Ce qui représente un exemple d'action du groupe sur un espace X avec x  X . . Il y a une infinité d'actions possibles, ne serait-ce que du groupe sur lui-même. Les actions sont définies par des axiomes.

(53)

En considérant le vecteur colonne :

(54)

où x représente par exemple les vecteurs :

(55)

(56)

vérifie les axiomes de l'action de groupe. On peut alors faire une multiplication à gauche de la matrice carrée représentant l'élément du groupe, avec une matrice ligne y , en se demandant si c'est aussi une action.

(57)

La réponse est non. Ce n'est pas une action de groupe : cela ne satisfait pas les axiomes donnés ci-dessus. C'est alors ce que j'aime appeler une "anti-action", obéissant alors aux "anti-axiomes" suivants :

(58)

La mathématicien dira qu'il n'est nul besoin d'invoquer ces "anti-actions" et qu'il n'y a qu'un jeu d'axiomes. Certes. De même ce qui est considéré comme l'anti-action :

(59)

m étant un vecteur donné, une "anti-action de l'élément g du groupe G sur la matrice m", g-1 désignant la matrice inverse peut être traité comme une action de l'élément g-1 .

De même une "anti-action" n'est que la duale d'une action. Disons que cela m'est apparu commode d'introduire ce concept, pour des raisons didactiques.

 
A partir d'un groupe de matrices carrées, dépendant de n paramètres pi on peut fabriquer des matrices, en différenciant tous ces paramètres selon : dpi . Les matrices ainsi obtenues, constellées d'éléments dpi, ne constituent pas un groupe , mais ce qu'on appelle le "vecteur tangent au groupe : dg  (son "algèbre-de-Lie", qui au passage n'est pas non plus un véritable algèbre, mais passons..).

Le groupe peut donc agir sur "vecteur tangent" dg , au voisinage de l'élément neutre e du groupe", à travers "l'anti-action" :

(60)

On obtient donc le schéma :

(61)

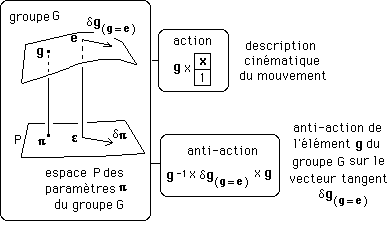
Mais une anti-action, c'est la duale d'une action. Or, quand il y a dualité, il y a conservation d'un produit scalaire S.

Souriau a donc cherché à construire une seconde action de groupe, celle du groupe sur son espace des moments . Mais cette action, dite action coadjointe ou essentielle , ne pouvait pas émerger directement. Il lui a fallu alors passer par cet intermédiaire qu'est ce que j'appelle "l'anti-action du groupe sur son vecteur tangent".

Ainsi l'action recherchée émerge en tant que duale de l'anti-action du groupe sur son vecteur tangent. Et la duale d'une anti-action, c'est une action, qui s'écrira :

(62)

où J sera le "moment" : une constellation de quantités qui sont des attributs d'un "point matériel", l'action en question, dite coadjointe , montrant comment ces attributs se modifient dans le mouvement.

 
Il existe un groupe, qu'on donnera plus loin, qui est une extension du groupe de Galilée, qui sera aussi donné plus loin, et qui s'appelle le groupe de Bargmann ( 1960). En appliquant cette méthode à ce groupe, on peut construire son moment JB et la manière dont le groupe agit sur celui-ci.

Souriau a coutume de dire :
 

Jolie image, empruntée à son ouvrage "Grammaire de la Nature". Le point matériel se déplace effectivement dans l'espace-temps (x,y,z,t). Ce faisant ses attributs évoluent, ceci étant décrit par cette action coadjointe du groupe sur son espace des moments.

  Retour vers le sous-sommaire "groupes et physique"