

 |
3
|
...Considérons l'espace 2d (x,y). Dans cet espace, une translation correspond au couple de scalaires ( Dx, Dy) et on a coutume d'écrire
On utilise alors l'addition . Pourrait-on se débrouiller pour coder la translation avec une ... multiplication ?
Considérons les matrices :
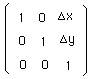
et l'action de groupe :
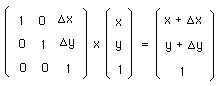
On note qu'il ne s'agit plus de la simple multiplication matricielle
g x r
mais de l'action de groupe :
![]()
On peut au passage envisager les translations dans trois, quatre dimensions et plus :

L'action de groupe correspondante est alors :
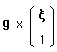
...Accessoirement le
groupe des translations est commutatif et l'élément neutre est
"la translation nulle". En 3d la dimension du groupe est trois, en 4d c'est
quatre.
Intérêt des groupes de matrices. Exemple : le groupe d'Euclide.
...L'intérêt d'un groupe de matrices, c'est qu'on peut négocier simultanément plusieurs choses, qui jusqu'à là semblaient d'essences différentes, par exemple rotation et translation. Il suffit alors de considérer les matrices :
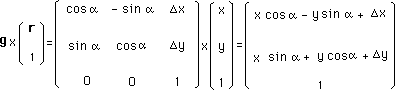
et faire agir la matrice élément du groupe sur le vecteur colonne pour constater que ceci équivaut à la combinaison d'une rotation d'un angle a et d'une translation selon le vecteur (Dx, Dy).
...Comme on le voit la matrice g n'agit pas "directement" sur les points (x,y) de cet espace 2d, mais à travers ce qu'on appelle une "action de groupe", qui obéit à certains axiomes.
...Ainsi un groupe "agit" et "transporte", en l'occurrence des points. Il s'agit là du groupe d'Euclide. Lié à un espace 2d (x,y), ce groupe est défini par trois paramètres. C'est g (a, Dx, Dy) : la dimension de ce groupe est 3. En particularisant :
g (0, Dx, Dy) représente le sous-groupe des translations.
g (a, 0, 0) représente le sous-groupe des rotations autour de l'origine.
g (0, Dx, 0) le sous groupe des translation parallèlement à une droite (l'axe OX).
...Le groupe d'Euclide transporte des points qui ne possèdent pas,
en soi d'attributs (alors que les groupes de la dynamique confèrent
à un simple "point matériel" des "attributs" nommés masse,
énergie, moment, spin).
...Avec le groupe d'Euclide
on est obligé de considérer des ensembles de points. Comme si,
en chimie, les atomes n'étaient pas distinguables les uns des autres
et que seules les géométrie d'assemblages moléculaires
soient porteuses d'une information.
...Une figure géométrique, triangle (considéré
comme un ensemble de trois points, ou de trois segments), carré (considéré
comme un ensemble de quatre points, ou de quatre segments) peuvent être
transportés par le groupe. C'est là qu'intervient l'idée
fondamentale d'espèce. Deux "objets" seront dits de la même
espèce s'il existe un élément du groupe qui permette
de les amener l'un sur l'autre.
Vis à vis du groupe d'Euclide des carrés ayant même côté a forment une espèce :
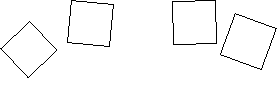
...Si les côtés a et b sont différents, ces objets ne sont pas de la même espèce. Il n'existe pas d'élément du groupe qui permette de passer de l'un à l'autre.
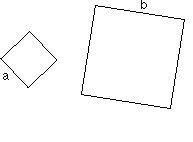
ces carrés ne forment pas la même espèce. .
Euclide ne permet pas les homothéties . Pour pouvoir le gérer, il faudrait passer à un autre groupe, celui de Descartes :
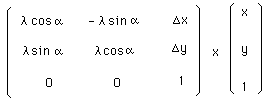
groupe à quatre paramètres g ( l, a , Dx, Dy) , l étant un coefficient d'homothétie. Donc la dimension de ce groupe est 4.
A partir de là on imagine bien qu'il puisse y avoir un groupe d'Euclide agissant sur des objets en trois dimensions.
...Il ne s'agit pas de se lancer dans un cours complet sur les groupes, mais de sentir quelques idées. Qu'est-ce que la zoologie? Une science consistant à étudier les animaux et à les classer. Si on se limite à la forme, le groupe d'Euclide permet de classer les lapins adultes. Il faudra recourir au groupe de Descartes pour pouvoir classer dans une même espèce des lapins de tailles différentes, vu qu'il n'existe pas d'élément du groupe d'Euclide (3d) qui permettre de passer d'un petit lapin à un grand lapin.
...Vous souriez ? Vous avez tort. Vous avez peut être, dans votre appartement ou maison, quelque bébé en cours d'apprentissage, qui joue dans un coin. Vous lui avec donné un jouet classique et il s'efforce de faire entrer dans une sorte de boite des formes : cylindres, cubes ou primes à base triangulaire.
...Qu'est-il en train de faire ? Il se familiarise avec le groupe d'Euclide, en 3d. Il classe des objets par espèces, ce qui lui permettra ultérieurement de les reconnaître, de faire de la "reconnaissance de forme".
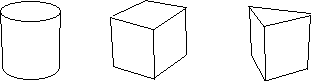
...Bien qu'ils soient de couleur différentes, le bébé vérifie qu'il existe bien des actions de groupes ( des transports de ces objets dans l'espace 3d) qui permettent d'amener le cylindre A et le cylindre B en coïncidence, en utilisant le crible qui est la "forme en creux" de ce cylindre, ou de ce prisme : le passage d'entrée vers le compartiment de sa boite de classement. Il apprendra ainsi que ces cylindres A et B , vis à vis du critère forme (groupe d'Euclide), appartiennent à une même espèce.
