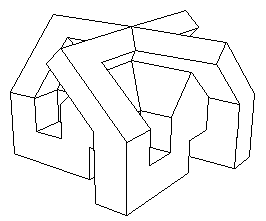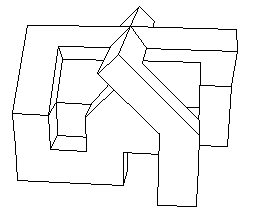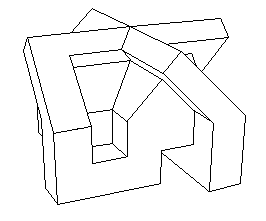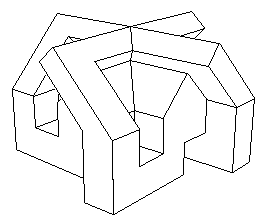
...Vous avez sans doute été intrigué par cet objet bizarre. C'est un travail qui a plus de dix ans. Au rayon maths je ne tarderai pas à installer une présentation d'un sujet vedette des mathématiques contemporaines : le Retournement de la Sphère. Il se trouve, et vous le découvrirez dans cette section, qu'on peut retourner une sphère recto-verso, en conservant la continuité de son plan tangent et à condition de lui donner la possibilité de s'auto-traverser. J'ai participé à cette aventure, dansles années soixante-dix et j'ai été le premier à en donner une description graphique lisible (Pour la Science, janvier 1979). Mais dans ces conditions, si une sphère peut se retourner, un cube peut en faire autant. Le retournement du cube n'est pas encore inventé. C'est un sujet de recherche. Peut-être certains d'entre vous trouveront-ils des éléments de cette transformation. Toujours est-il que l'objet ci-dessus est le modèle central de la transformation. Je mettrai un découpage qui vous permettra de le construire et de le poser sur votre bureau. Dans un tel "modèle central" le cube est à moitié retourné. Supposons que sa surface ait présenté une couleur verte à l'extérieur et jaune à l'intérieur. Une succession de transversements des nappes amène le cube dans cette configuration "à quatre oreilles", version polyédrique du "modèle central ouvert" de Bernard Morin.

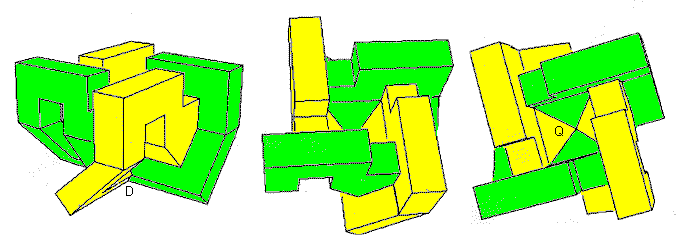
...Ce cube montre donc un reste de ce qui était son extérieur (les "oreilles" vertes) et ce qui est apparu à la suite de ces transformations (les "oreilles" jaunes, qui correspondent à l'intérieur de l'objet). Le lettre D indique le point double du modèle. La lettre Q le point quadruple (où se croisent quatre nappes). On sait qu'il existe une infinité de déformations successives permettant de transformer notre cube vert en cet objet à symétrie quaternaire. Ces déformations ne sont que les versions polyédriques de l'infinité de déformations permettant de transformer une sphère (verte à l'extérieur) en modèle à quatre oreilles (deux vertes et deux jaunes). Reste à trouver, à inventer les étapes intermédiaires les plus simples, avec un minimum de faces, de sommets et d'arètes. Voilà un joli travail de recherche.
...Au passage ceci démontre que le cube peut être retourné recto-verso (comme la sphère, dont il n'est que la version polyédrique) . En effet, pour qui disposerait de la séquence évoquée, il suffirait de faire effectuer au modèle une rotation de 90° selon son axe de symétrie, puis de reprendre la séquence à l'envers pour aboutir à un cube ... jaune.