22)
Black holes do not exist.
Where
the black hole model does come from ? From the null second member field
equation. Paradoxically such very dense object rises from an equation which was
initially built to describe empty regions of the Universe. The Kerr metric does
not bring so much : the object becomes more complex, that’s all. Rotation
brings an azimutal frame-dragging phenomenon, which means that the speed of
light is different if one looks forward or backward with respect to the
spinning movement. Whatever is the technique you choose, the things become
frankly pathological when you pass the horizon and get in. At the centre lies
“the singularity”. Let us start with an exercise. Consider the 2d metric (a).
If we consider r as a radial distance and j as a polar angle, we get problems for r < Rs. But if we
introduce the change (b) the expression of the metric becomes (c). All
pathologies disappear. Moreover this surface can be imbedded in R3 : the
meridian equation is (d). See figure 25 where we have figured a geodesic. This
illustrates the fact that a pathology can depend on a wrong choice of
coordinates and on a wrong choice of topology.
In the 3d example we have computed (plane) geodesics ( see figure 26 ) which are projected on the initial (r,q,j) representation space. We get a “throat sphere” linking two Euclidean 3d spaces. There is nothing inside. Space for r < Rs has no physical meaning. If we would try to compute geodesics in that place, we would find an imaginary solution.
![]()
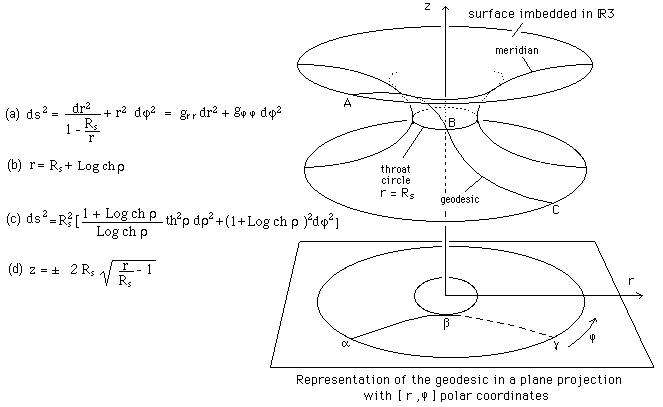
Fig. 25 : 2d metric
of a surface with a “bridge” linking two folds.
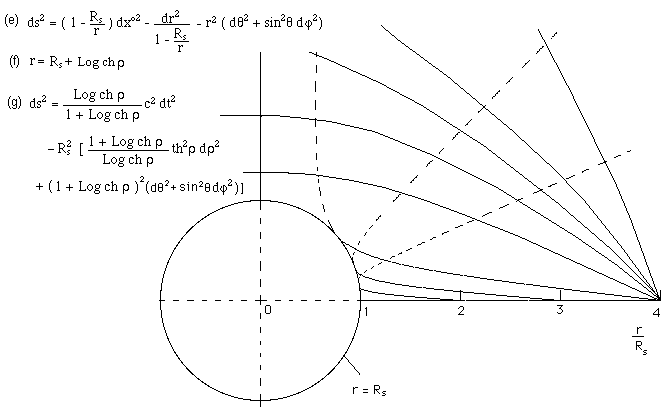
Fig. 26 : 3d metric
hypersurface with a “space bridge”.
Geodesics.
![]()
Classically, one introduce
a proper time s (j) and a “time-coordinate t (i). Then the study of radial
geodesics gives two differential equations (k) and (l), whose solutions
correspond to curves (m), fig. 6.2, reference [52].
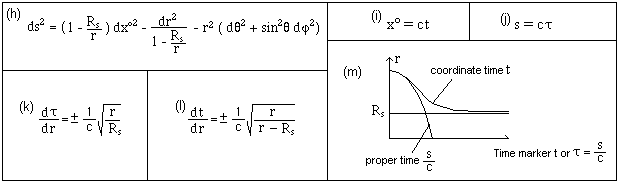
The
curves shown on figure (m) are the basis of the black hole model. One
identifies the coordinate t to the proper time of a “distant observer” so that
the free fall time of a test particle, towards the Schwarzshild Sphere become
infinite for him. Let us show that this is completely due to this peculiar
choice of time coordinate. In [54] 1925 Eddington suggested a new time-marker (p).

Following,
the study of corresponding radial geodesics.
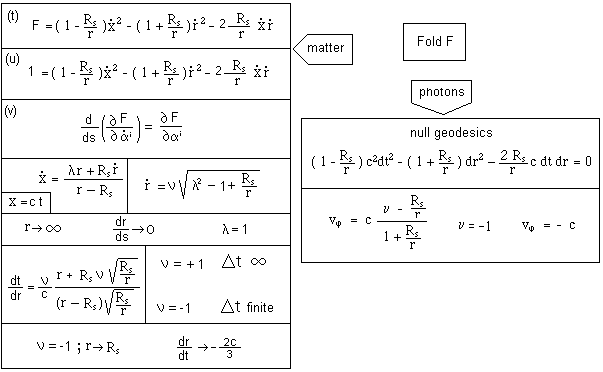
We
use Lagrange equations. On the right we
see that the speed of light, following radial paths has two values. ( nu = - 1 ) corresponds to centripetal
paths : the speed has a constant value – c. Similarly (left) the transit time
from a distant point to the Schwarzschild sphere depends on the orientation of
the paths. Centripetal ( nu = - 1 ) free fall time is
achieved in finite time interval Dt . Oppositely a centrifugal path ( nu = + 1 ), starting from the Schwarzschild sphere gives an infinite time
interval, so that the Schwarzschild sphere works like a one-way membrane. This
corresponds to a radial frame-dragging
effect. This is not a reason to reject this interpretation of the
Schwarzschild geometry. In effect we find a similar phenomenon in the Kerr
metric ( azimutal frame-dragging).
Next, the classical expression of the Kerr metric. We see that we get two
distinct values for azimutal speed of light. Depends if we consider light
following the rotation or going backwards.
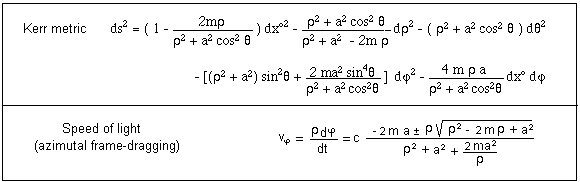
We
can give a new interpretation of the Schwarzschild geometry, through a
space-bridge linking two folds F and F. If the fold F corresponds
to the twin fold, the time coordinate t = - t ( T-symmetry). From
section 19 we know that this T-symmetry goes with a mass-inversion, so that
when a positive mass passes through the Schwarzschild sphere, considered as a
throat surface, the sign of it becomes negative. The conjugated geometry, as
presented in section 13 corresponds to change Rs into – Rs.
Then we introduce the following Eddington-like time marker change :
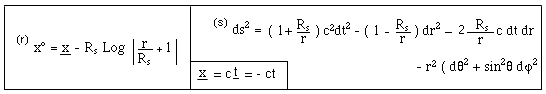
Still using Lagrange’s equation we study the radial geodesics system and build a link between the two folds.
![]()
But the inverse paths
requires an infinite time, so that it is a one-way passage from a Universe to
the other. Here again we find a frame-dragging effect, in the opposite
direction.
During the transit the proper time flow is
unchanged : ds > O . This makes the black hole model questionable. In effect, according to
this new interpretation of the Schwarzschild geometry such space bridge can
swallow in a very short time ( » 10-4 sec) unlimited
amounts of matter. By the way, an analysis based on the Kerr metric, although a
little bit more complicated gives similar results.
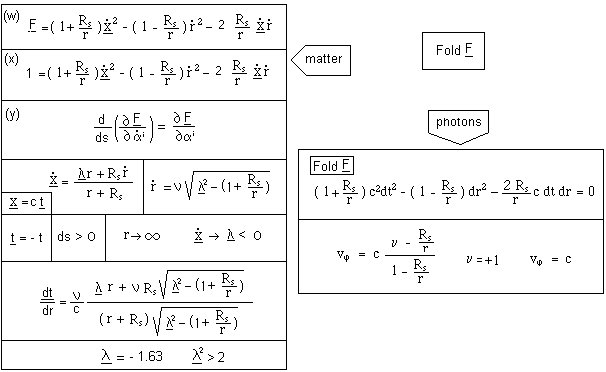
Following,
the solution of the geodesic systems.
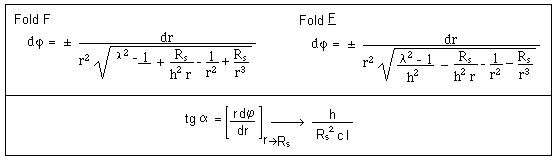
How
to figure such paths ? We can use the initial ( r , q , j ) representation space. Then we get
the above system of differential equations and the schema of figure 27 .
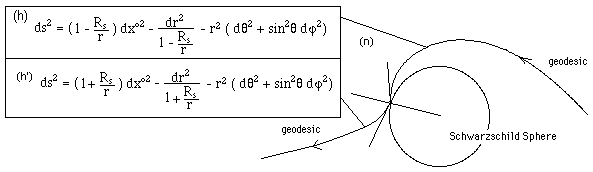
Fig.27 : Income
and outcome geodesics.
The geodesic seems to “bounce” on the
Schwarzschild sphere, as shown of figure 28 too.
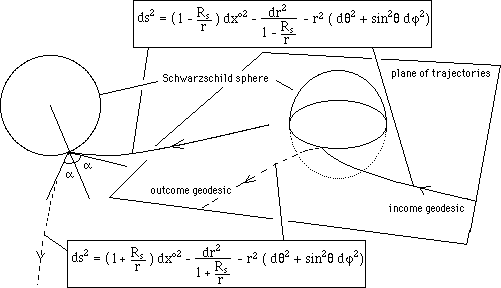

But
all that comes from such naïve Euclidean representation of the path. Using the
following change of space marker :
![]()
The
expression of joint metrics become :

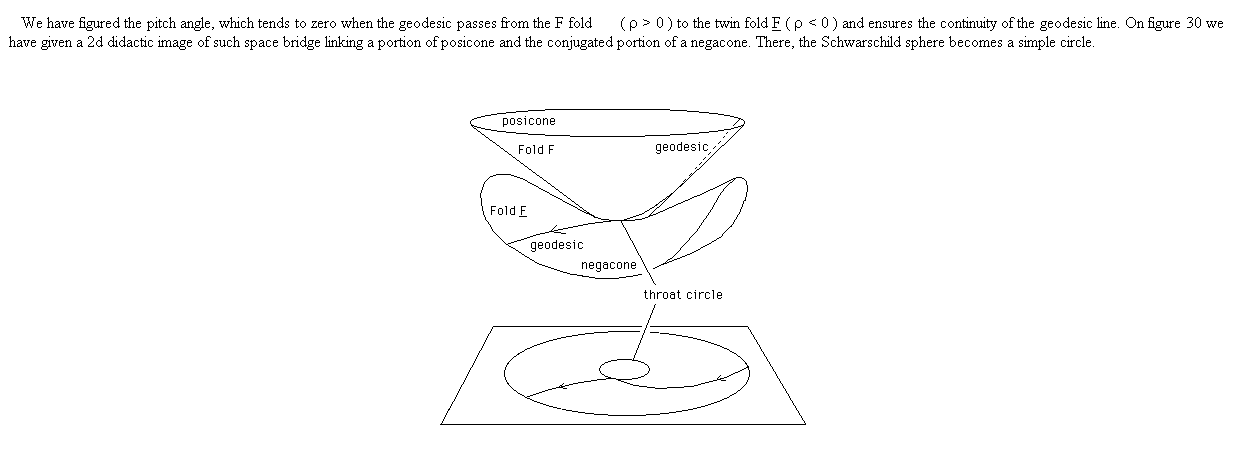
Fig. 29 : Didactic image of a fast flow space bridge.
References.
[1] J.F.Augereau
: « Si la matière sombre dévie les rayons lumineux, c’est donc qu’elle
existe” (If dark matter bends light rays it shows it does exist). Le Monde, March 17 th 2000.
[2] Interview of B.Fort in Ciel et Espace, june
2000.
[3] J.P.Petit : The missing mass effect. Il Nuovo Cimento, B , vol. 109,
july 1994, pp. 697-710
[4] J.P.Petit, Twin Universe Cosmology. Astrophysics and Space Science.
Astr. And Sp. Sc. 226 : 273-307,
1995
[5] Zel'dovich Ya.B., Astrophysica 6. 319 MNRAS 192, 192(1970)
[6] Doroskhevich A.G. MNRAS 192, 32 (1980)
[7] Klypin A.A & Shandarin S.F. MNRAS 204, 891 (1983)
[8] Centrella J.M. & Mellot A.L. Nature 305, 196 (1983)
[9] Mellot J.M. & Shandarin S.F. Nature 346 , 633 (1990)
[10] Shandarin S.F. In Large Structures of the Universe, ed. J.Audouze, M.C.
Peleton and A.Szalay, 273. Dordrecht : Kulwer (1988).
[11] Kofman.L.A., Pogosyan D. and Shandarin S.
MNRAS 242, 200 (1990)
[12] Peebles P.J.E. Principles of Physical
Cosmology, Princeton University Press (1993).
[13] M.Myamoto and R.Nagai Publ. Astrom. Soc. Japan 27, 583, 1975
[14] J.Binney and S.Tremaine, "Galactic Dynamics", Princeton University
Press, Princeton, 1987. [16] Bahcall J.N & Soneira R.M. APJ. S 44 p. 73 1980
[17] Bahcall J.N. , Flynn A and Gould A. APJ 389 p.234 1992
[18] B.Lindblad, Handbuch der Physik 53,
(1959) 21
[19] C.C. Lin and F.H.Shu : Astrophysics and Gen. Relat. Vol.2 Gordon and
Breach Sc. Publ. 1971, p. 235
[20] Toomree A. (1981) The structure and dynamics of normal galaxies. Cambridge
University Press, p.111
[21] Toomree A. and Toomree J. (1972) Astrophys. J. 178, 623
[22] A.Toomree, Ann. Rev. Astronom. Astrophys. 15 (1977) 437
[23] E.Athanassoula : Companion driven spirals and bars. International
Astronomic Union. Symposium n° 146 (1991)
[24] A.Toomree Astrophys. J. 158
(1969) 89
[25] R.H.Miller and B.F. Smith, Astrophys. J. 277
(1979) 785
[26] F. Hohl, Astrophys. Sp. Sc. 14
(1971) 91
[27] Holmberg E. (1941) Astrophys. J. 94,
385
[28] B. Sundelius and K.J. Donner : Interaction galaxies, Dynamics of Disk
Galaxies (1991) Sundelius ed. p. 195
[29] S. Engström : Feature velocitys in numerical simulations. , Dynamics of
Disk Galaxies (1991) Sundelius ed.p. 332
[30] A.Toomree Ann. Rev.
Astron. Astrophys. 15 (1977) 437.
[31] F.Bouchet and L.Hernquist : Cosmological
simulations using theoretical tree methods. Astr. Jr Suppl. Series 68 , pp. 521, 538, 1988.
[32] F.Bouchet, L.Hernquist and Y.Suto : Application of the Ewald method to
cosmological N-body simulation. Apj. Suppl. Series 75 , pp. 231-240, 1991
[33] A.Sakharov : "CP violation and baryonic asymmetry of the
Universe". ZhETF Pis'ma 5 :
32-35 (1967) : Traduction JETP Lett. 5
: 24-27 (1967)
[34] A.Sakharov : "A multisheet Cosmological Model" Preprint
Institute of Applied Mathematics, Moscow 1970
[35] A.Sakharov : "Cosmological Model of the Universe with a time-vector
inversion". ZhETF 79 : 689-693
(1980) : Traduction in Sov. Phys. JETP 52
: 349-351 (1980)
[36] A.Sakharov : "Topological structure of elementary particles and CPT
asymmetry" in "problems in theoretical physics", dedicated to
the memory of I.E.Tamm, Nauka, Moscxow 1972 pp. 243-247
[37] Green M.B. & Schwarz J.H. Nucl. Phys. B181 , 502-530 (1981) ; B198
, 225-268 (1982) ; Phys. Lett. B , 444-448 (1982)
[38] Green M.B. Surv. High Energy Phys. 3
, 127 (1982)
[39] Gross D.J. , Harvey J.A. , Martinec E. & Rohm R. , Phys. Rev. Lett. 54, pp 503-505 (1985)
[40] Kolb E.W. , Seckel D , Turner M.S. : The shadow world of superstring
theories, Nature Vol. 314, april 1984 pp. 415-419
[41] P.C.W.Davies & J.B.Brown : Superstrings, Cambridge University Press
1988
[42] Abdus Salam, Nuovo Cimento 5 ,
299 (1957)
[43] Nima-Arkani Ahmed, Savas Dimopoulos and Georgi
Dvali : "Les dimensions cachées de l'univers", PLS oct 2000 n° 276
pp. 56-64
[44] J.P.Petit : An interpretation of cosmological model with variable light
velocity. Modern Physics Letters A, Vol. 3, n°16, nov
1988, p.1527
[45] J.P.Petit : Cosmological model with
variable light velocity: the interpretation of red shifts. Modern
Physics Letters A, Vol.3 , n° 18, dec. 1988, p.1733
[46] J.P.Petit & Maurice Viton : Gauge
cosmological model with variable light velocity. Comparizon with QSO
observational data. Modern Physics Letters A Vol.4 , n°23 (1989) pp. 2201-2210
[47] P.Midy & J.P.Petit : Scale Invariant
Cosmology. The international Journal of Modern Physics D, Vol.8 June 1999
pp.271-280
[48] E.A.Milne : Kinematic
Relativity Oxford 1948.
[49] J.D.Anderson, P.A.Laing, E.L.Lau, A.S.Liu,
M.M. Nieto and S. Turchev : Indication for Pioneer 10/11, Galileo and Ulysse
Data, an an Apparent Anomalous, Weak, Long-Range Acceleration. Phys. Rev.
Letters : 81 31 August 1998.
[50] G.J.Stephenson Jr. , T.Goldman, Phys. Rep. 205, 211 (1992) ; 216,
343 (1992).
[51] M.N. Nieto and T.Goldman, Phys. Re. 205, 221, 1991; 216,
343.
[52] R.Adler, M.Bazin & M.Schiffer : Introduction to general
relativity, Mac Graw Hill book, 1975, chapter 10, section 10.5 : Classical
limit of gravitational equations, p. 345.
[53]
J.M.Souriau, Structure des Systèmes Dynamiques, Ed. Dunod 1970, France & Structure of Dynamical
Systems. Birkhauser Ed.
Boston-Zurich 1997.
[53]
J.P.Petit : Univers énantiomorphes à flèches du temps opposeés
(Enantiomorphic universes with opposite time arrows). Comptes rendus de
l’Académie des Sciences de Paris, t. pp. 1977
[54]
Eddington S.A : : A comparizon of Withead’s and Einstein’s formulæ. Nature 113 : 192 (1924).
