Theoretical
physics is in a big crisis since mode than 30 years. A lot of papers were
published many years ago about magnetic monopole, but no one appeared. The
existence of supersymetric partners has not been proved yet. Nobody knows what
a “graviton” could be. When scientists tried to evidence the proton’s decay,
this last did not cooperate. Almost all that new telescopes bring is still e
complete mystery. Nobody knows what are QSO, gamma flashes and how it works. Giant
black holes are strangely silent, and so on. Superstring is nothing but a new
fashion, in spite thousands papers published in this “new field”. Superstring
world is a strange play field in which physics seems desperately absent. In the
following we give the first geometrical description of antimatter. As
J.M.Souriau uses to say, group theory
is the most basic tool we have to deal with physical phenomena. A natural
action of a Lie group is its coadjoint action on its Lie algebra, as introduced
by J.M.Souriau in 1970 [53]. The dimension of a group G is the number of parameters it depends on.
This is also the number of components of its moment J . The Lorentz group L is a six-dimensional group, which owns four
connex components. Introduce the four elements group omega, in its matrix representation (a). Then we can
built the complete Lorentz group L from its neutral component Ln, through a direct group product
(b), where (c) is the matrix representation. A new semi-direct product
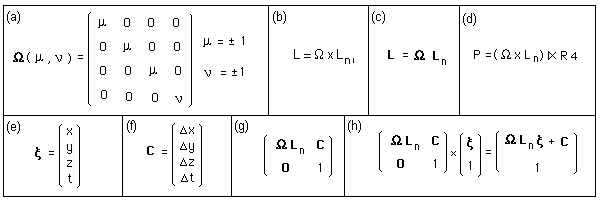
(d) gives the Poincaré group. Introduce the event-quadrivector (e) and the space-time translation vector C : (f).We
can give a matrix representation (g) of the Poincaré element. In (h) its action
on space-time. But this one hides a more important action : the coadjoint
action of the group on its ten components moment space J (the Poincaré group owns ten dimensions).Souriau
writes this moment
J = { E , p , f , l }
E is the energy, p the impulsion, f the “passage” an l
the spin. It is convenient to introduce, following Souriau, an
antisymmetric matrix M : (a) and the quadrivector
impulsion-energy P : (b). The calculation of the dual of the
action of the group on its Lie algebra gives the action on the momentum { (c) ,
(d) }.
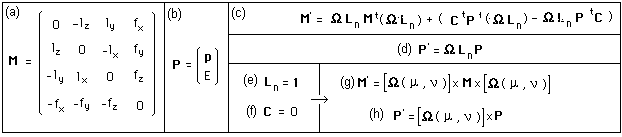
Now, il we want to evidence
symmetries I , P , T and PT we choose
(e) and (f). The the coadjoint action becomes { (g) , (h) } , which gives :
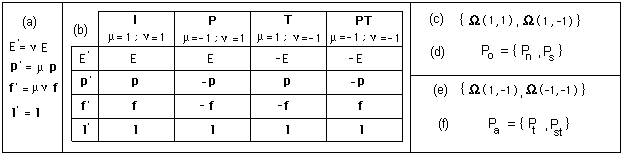
As
pointed out in 1970 by J.M.Souriau, with the matrixes (c) we build the
orthochron subgroup Po :
(d), composed by two connex components : the neutral one Pn and by the space-inversion
component Ps. The
terms of these two components do not inverse the sign of the energy E. Conversely, the matrixes (e)
produce the antichron subset, whose terms inverse the sign of the energy, so
that time-inversion goes with energy inversion, i.e. mass-inversion, if the
particles own one. As a conclusion we see that negative mass and negative
energy arise from the dynamic Poincaré group description, referring to
relativistic mass-point movements. Now, we are going to extend the Poincaré
group, considering :
![]()
We
introduce the matrix (a) and (b). Then we give a matrix representation of the
group, acting (e) on a bundle Z 2 x U(1) x R4. In (f) we get the geometrical
expression of the C-symmetry. The fifth dimension (c) is compact. Then any
element of the group corresponding to choices (f) implies a
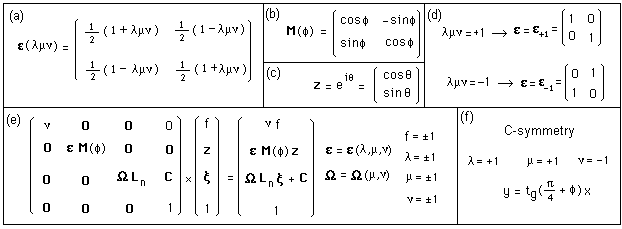
symmetry with respect to
the indicated straight line. The calculation of the coadjoint action of the
group on its momentum shows no peculiar difficulty. As pointed out by Souriau
in 1970 the addition compact dimension q goes with a quantified additional scalar,
identified to the electric charge q. The action on the part of the moment
corresponding to Poincaré does not change. The action on the electric charge
gives :
![]()
Particles are describes in
terms of orbits of the group. Some own a positive energy and others a negative
one. f can be considered as a fold index.
f = +1 refers to fold F f = -1 refers to fold F
Wet get a geometrical twin
structure. The action is simply :
f ’ = n f
This
can be summarized on figure 21.
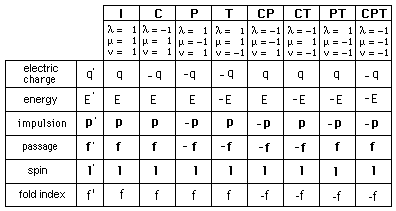
Fig. 27 : Impact
of symmetries on the momentum components.
Notice that ( nu = - 1 ) refers to antichron terms of the group. A particle and its
movement correspond to a peculiar element of the momentum. Antichron terms
transform orthochron movements into antichron ones and reverse mass and energy.
As space time is composed by two separate folds F and F , encounters of
opposite energy particles can be avoided if we put positive energy particles in
one fold, F for example, and negative energy in its twin fold F. This
physical description is consistent to the group properties.
21) PT-Symmetry and CPT-symmetry.
As pointed out by Souriau in 1970, all symmetry
which includes a T-symmetry reverse the energy and the mass. If we consider a
normal particle, with mass m and electric charge q , its CPT-symmetrical owns
negative energy and mass. Feynman showed that the PT-symmetrical of a particle
behaved as an antiparticle, but, according to Souriau’s result, it owns
negative mass and energy.. From above, we have built a new description of the
Universe as composed by two twin entities. The first is a fold F, supposed to
be ours, filled by matter and Dirac-antimatter, C-symmetrical with respect to
the first. In the second fold F the matter-antimatter duality holds too.
Its matter is CPT-symmetrical with respect to ours, while its antimatter
identifies to Feynman one. As a whole, the two folds are CPT symmetrical. This
goes with initial Sakharov’s ideas ( [33]
to [36] ). The initial work of
the author, devoted to twin Universe cosmology, was published in 1977.
22) Leaking neutron star model : a challenger to black hole model.
Classically the criticity of a neutron star is
based on a geometrical criticity. A constant density sphere, surrounded by
void can be described by two linked Schwarzschild metric (internal and external).
These expressions have been give in section 7. Both become critical when the
neutron star’s radius tends to its associated Schwarzschild radius. Tolmann,
Oppenheimer and Volkov derived ( see [52], eq. 14.22 ) a famous “ TOV equation
” giving pressure versus radial distance in a neutron star.
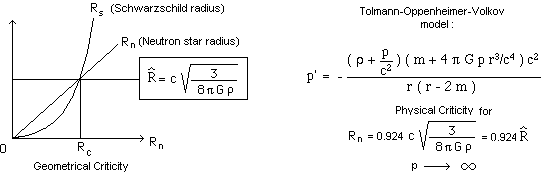
Fig. 28 : Left, geometrical criticity. Right : physical
criticity.
The calculation shows that, before the
geometrical conditions are reached, a physical criticity occurs : pressure tends
to infinite at the centre of the star (left).
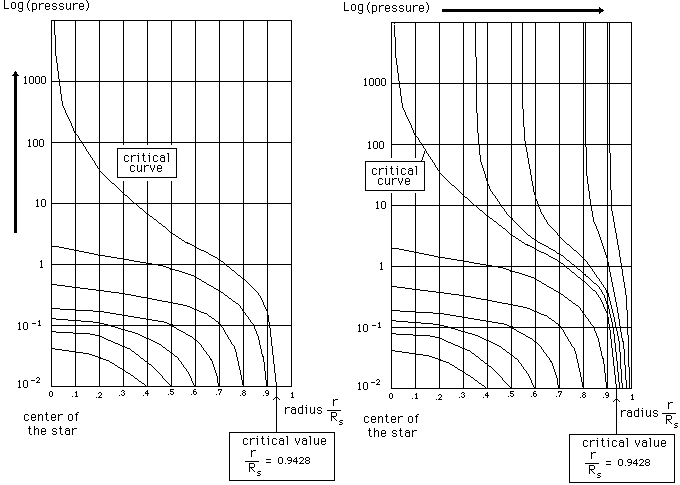
Fig. 29 : Pressure
versus radial distance in a neutron star.
We
are going now to make assumptions. In section 15 we tried to describe the primitive
stage of the Universe, going backward in its past. In order to explain its
great homogeneity we introduced a variation of the constants of physics, during
the radiative era. By the way, this exploration is still very hazardous. We
only tried to give new insights on the question : “what happens when we look at
the distant past of the Universe ?”. I think we don’t own all the keys. I will
just expression an opinion. I would think that when the pressure reaches a
critical value (to be determined) our Universe becomes linked to its twin
which, as A.Sakharov suggested “lies in its past”. Although it is still
confused, I admit, I think that our universe interacts with its past, which
would extends over some sort of space-time bridge. Sakharov Thought that our
Universe and its twin were linked. I add they would be interacting, everywhere,
all the time. That’s for the arrow of time is found to be reversed in the twin,
from section 19. That’s for the twin’s atoms seem to own a negative mass and
repel ours. For us, they just live backward in time, that’s for, according to
Souriau’s works, their apparent mass
is negative. By analogy I would think that when physical criticity is reached
at the centre of a neutron star, the local values of the constants of physics
change drastically. Such condition would “reproduce” locally the “Big Bang
conditions”. A spaced bridge would open, sucking matter at relativistic
velocity. Such “soft scenario” would occur when the matter’s flux due to the
solar wind of a companion star achieves critical conditions at the centre of
the star. Then a steady state can be geometrically described, using the four
Schwarzschild metrics. For fold F :
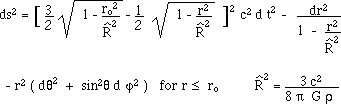
For the adjacent, conjugated
region of the twin fold F:
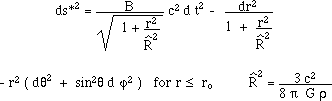
One can study the geodesic
systems and link them, through a space bridge whose single parameter is its
area. Tiny space bridges can absorb the matter corresponding to stellar wind of
a companion star, for, close to it, the density is enormous and the velocity
relativistic. On figure 24 a 2d didactic image of the model.
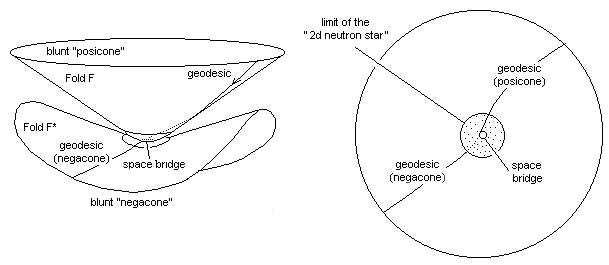
Fig. 30 : 2d
didactic image of a sleaking neutron star (SNS).
A
violent inflow of matter, due for example to more eruptive phenomena of a
companion star or to the fusion of two neutron stars, forming a binary system,
could produce fast opening of a space bridge, as suggested on the right of
figure 24. The explanation of gamma bursts could lie there. This model challenges the black hole model. We will
see further how this last is questionable. Something goes wrong with this
black hole model. There are too few candidates and everybody knows that a
slight error about distance evaluation can convert such black holes candidates
into simple neutron stars. There is no undeniable proof of their existence.
People only believe in. They always
said : “what could you imagine else ?”. Look at the beginning of the paper.
We evoked the issue of the Journal le Monde in which Fort and Meillier presented
a coloured 3d map of dark matter and the journalist, enthusiastic, titled
[1] : “The dark matter does exist : it bends the light
rays”. But what about the “dark clusters” [2], discovered by the same people, which “attract the light rays, bend it,
but apparently repel the ordinary matter”. If this is confirmed they would
be made, as suggested by Fort, exclusively of “exotic matter”, and if they
are, what is that stuff ? What about the acceleration of the space probes
[49], that a dark matter distribution cannot explain ? Today people need to find giant black holes at the centre
of galaxies, in order to justify the dynamical parameters of such regions.
But these giants seem very silent, like sleeping beauty, don’t they ? Some
suggested they could be “satiated black holes”. How long time will we try
to answer new problem just inventing new name ?
