7) Gravitational lensing due to negative mass matter.
...In classical general relativity the
(steady) geometry of space-time, in and around a sphere filled by constant
density matter, and surrounded by void is described by two joined metrics. The
first is the "internal Schwarzschild metric" :
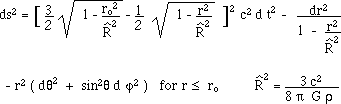
with the condition :
![]()
and the second the
"external Schwarzschild metric":
![]()
...Classical gravitational lensing is
computed with the second, where m, a simple integration constant, is chosen
positive. Then the plane trajectory of a massive particle is given by
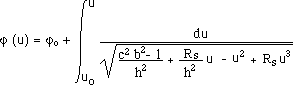
where phi is the polar angle, and u the inverse of radial distance r, with respect
to the geometric centre of the system. The photons obey :
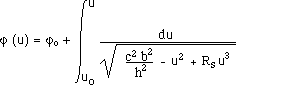
where c is the light
velocity, h and l paths parameters. This gives the classical schema of figure
10-a where the central mass is reduced
to a simple mass-point. Now, have a look to (16) and (18). We can change the sign of the mass density and R s into – R s. Then we
get the :
(16bis)
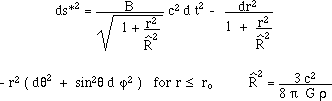
![]()
...These solution can be linked and describe the geometry in and out a sphere filled by negative mass. The first is solution of the field equation
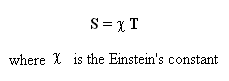
The second comes from S = 0 . As introduced in 1995 in reference [3] we get a
negative lensing effect. See figure 10-b
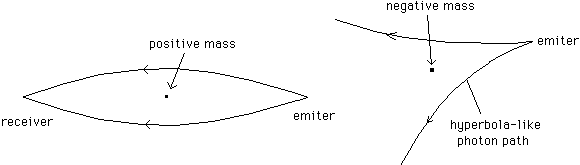
Fig. 10-a :
Positive gravitational
Fig.10-b : Negative gravitational
lensing effect lensing effect
...Notice we may
now use the internal solution for photons can cross a negative mass clump,
according to our assumption (like neutrinos can cross the sun. But we have no
telescopes using neutrinos). Now, examine the impact on observations. The first
one is the reduction of the luminosity of large redshift galaxies, by negative
gravitational lensing effect due to twin matter clumps. As the matterfact, we
find many faint galaxies at large distance. The classical interpretation
consists to say that dwarfs galaxies form first, then merge to give heavier
objetcs. Negative lensing provides an alternative explanation. Now, let us show
that negative lensing, due to surrounding twin matter, can explain observed
strong lensing effects, around galaxies and clusters of galaxies. First, notice
than any homogeneous distribution of matter, with positive or negative density,
does not induce gravitational lensing. Only non-homogeneous distribution dot
it. Let us figure schematically a galaxy imbedded in some sort of hole in an
homogeneous twin matter distribution. See fig. 11-a.
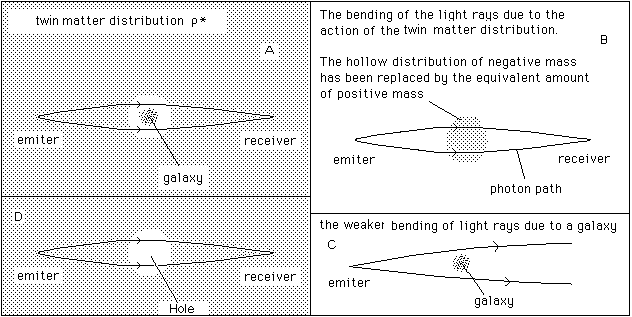
Fig. 11 :
Combination of positive (due to the
confined object) and negative (due to the surrounding twin matter) lensing
effects. Reinforcement of the global effect.
... We have
schematised the reinforcement of the gravitational effect due to twin matter
surrounding a spheroidal mass M ( spheroidal galaxy or spheroidal cluster of
galaxies). As shown in section 18 the gravitational field due to a spheroidal
hole in a constant density negative mass distribution is equivalent to the
field due to a constant density sphere, filled by positive mass (figure 11-b).
On figure 11-c we have figured the contribution of the positive mass M to the
gravitational lensing effect. The main effect (figure 11-c) is due to the hole,
which focuses the light rays. On figure 11-a we find the two effects, combined.
As a conclusion the observation of strong gravitational lensing effects at the
vicinity of galaxies or clusters of galaxies is not the final proof that some
positive mass invisible dark matter is present. There is an alternative
interpretation : the object could be surrounded by negative matter, which
focusses the light rays.
8) Exotic matter or exotic geometry ?
...As said
above, physicists have difficulty to stand the idea that negative mass could
exist in our universe. By the way, the classical standard model does not bring
all the answers. For example, nobody knows where the primeval antimatter is
gone, so that half part of the universe is missing. The question became so
embarrassing that today scientists just choose to avoid it. In 1967 A.Sakharov
suggested that some "twin universe" would have been created during
the so-called Big Bang, where the arrow of time could be reversed
([33],[34],[35]&[36]) . The idea of a couple of universes interacting only
through gravitational force is in progress, see a recent paper of Nima-Arkani
Ahmed (Dept. of Phys. of Berkeley U.), Savas Domopoulos (Dept. of Phys of
Stanford U.) and Georgi Dvali (Dept. of Phys. Of new-York Univ.), reference
[43] and references [37] to [42] .
...Assume the universe is the two-folds cover
of a M4 manifold.
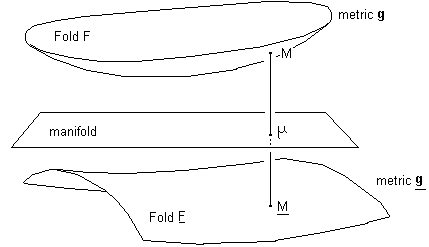
Fig.12 : Two
folds cover of a manifold.
...We get a point-to-point mapping, linking two "conjugated points" M and M , which can be described by a same system of coordinates
![]()
We can give this non simply connected two-folds cover a metric structure (similar to the two-points bundle of a manifold M4). We can give a manifold any number of distinct metrics. Each defines a metric space. The underlying manifold gives a point-to-point mapping, linking all the points of these metric spaces. We get two coupled metric spaces F and F.
Here we take two riemanian metrics with the same hyperbolic signature (+ - - - ). We call the metrics g and g . From these two metrics we can build geodesics systems but, as F and F and disconnected, the two families of geodesics are disconnected. As a conclusion, if these metrics give null-geodesics and if one assume that light travels along them in both folds, any structure of a given fold will be geometrically invisible from the other one. In classical General Relativity one considers a single fold, associated to the field equation (Einstein equation)
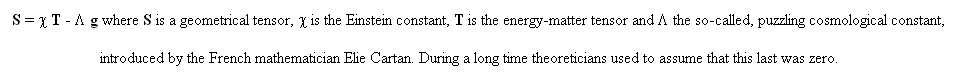
Then, non-steady solutions, corresponding to homogeneous and isotropic conditions give the Friedman models. Steady-state solutions, while spherical symmetry gives the internal Schwarzschild solution (16), from the equation
![]()
where T is a constant tensor field, inside a sphere whose radius is ro.
The external Schwarzschild solution (18) comes from S = 0 with spherical symmetry too. The choice of a field equation is an a priori choice. If metric solutions are asymptotically flat, Lorentzian, it ensures the validity of Special relativity in vacuum. If one makes an expansion into a series around a Lorentz metric, in steady state conditions, the field equation can be identified to Poisson equation
![]()
In addition, the Newtonian approximation provides the Newton law of
interaction. Friedman models, corresponding to solutions of the field equation,
provide a redshift, which is observed. Locally, the bending of light rays at
the vicinity of the sun as well as the precession of Mercury's perihelion are
observed too. But recently some discrepancy between Friedman models and
Hubble's constant measurements lead today the cosmologists to reintroduce a
non-zero cosmological constant, corresponding to some mysterious
"repulsive power of vacuum".
...Now, return to the two-folds structure.
Introduce two tensor fields T and T which are supposed to describe
the contents of folds F and F. From metrics g a
nd g we can
define derive geometric tensors S and S. We can link the four
tensors S , S , T , T into a system of two coupled
field equations, inspired by Einstein equation
9) First geometrical interpretation of
the dark matter phenomenon.
Consider the following
coupled field equations:
![]()
...Basically, they are identical, so that g identifies to g : the image of a geodesic of fold F becomes a geodesic of fold F. We get two "parallel" universes, which interact only through gravitational force. Dark matter can be composed by atoms, neutrons, protons, photons, identical to ours, except we cannot observe twin matter on geometrical grounds. If we study the Newtonian approximation, we get the following Poisson equation :
![]()
...In this model :
- matter attracts matter
- twin matter attracts twin matter
- matter and twin matter attract each other.
...But this does not solve all the
observational data : even if some geometrically invisible dark matter would lie
in the adjacent portion of our universe, near by the Abell 1942 cluster, this
does not explain why this attractive force field would not capture our own
galaxies and gas, lying in our fold of the universe. That's for we deal with
the following set of equations (reference [3] and [4] ) :
10) Second geometrical interpretation of
the dark matter phenomenon.
...Consider the following coupled field
equations system :
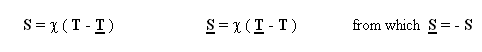
Notice this definitively
not imply g = - g . The Newtonian approximation
supports the assumptions of section 3. We get the following Poisson equation :
![]()
...We prefer to consider that the twin
universe, the twin fold, is filled by intrinsically positive mass matter and
that the minus sign in the field equation gives it the appearance of a negative
mass for an observer located in our fold. Then we may call it "apparent
mass". The symmetry of system (29) plus (30) makes the definition of
positive and negative energies purely arbitrary. What about the classical local
check of the RG ? In this new model :
- matter attracts matter,
through Newton law.
- twin matter attracts twin matter through Newton law.
- matter and twin matter repel each other through an "anti-Newton
law".
...The solar system is a very dense
portion of the universe. In the adjacent portion of the twin fold, twin matter
is pushed away. Then the system is very close to :

...The first equation identifies to
Einstein equation, so that all the classical verifications fit. . What about
gravitons ? Which path do they follow ? The answer is composed by two arguments
:
- Field equations provide macroscopic description of the universe, which
ignores the existence of particles and just gives geodesic systems.
- By the way : what's a graviton ?
Notice that recently [49], anomalous long-range (negative) acceleration has been evidenced for
space probes Pioneer 10 and Pioneer 11, at long distance from the sun (40-60
AU). An unmodelled acceleration, directed towards
the Sun, (8.09 ± 0.20 ) x 10-8 cm/s2 for Pioneer
10 and (8.56 ± 0.15) x 10-8 cm/s2 for Pioneer 11, was evidenced and described
as a not-understood viscous drag force.
Similarly, and unmodelled acceleration towards the sun was found for the probe Ulysse (12 ± 3 ) x 10-8 cm/s2. See complete
discussion in this interesting paper. The authors say : The paradigm is obvious : s is it dark matter or modification of
gravity ”. As the pointed out, if dark matter is called for explanation, it
would correspond to a total dark matter amount > 3 x 10-4 solar mass, which would be in
conflict with the accuracy of the ephemeris. A 3d neutrino model also did not
solve the problem [50]. Others try to modify the Newton law,
adding a Yukawa force [51]. But “this anomalous acceleration is too large to have gone undetected in
planetary orbits, particularly for Earth and Mars”. Then they focus on
available Viking probes data and conclude : “But a large error would cause inconsistency with the overall planetary
ephemeris…. if the anomalous radial acceleration acting on spinning spacecraft
is gravitational in origin, it is not universal. That is, it must affect bodies
in the 1000 kg range more that bodies of planetary size by a factor 100 or more
(…), which would be a strange violation of the equivalence principle”. An
alternative interpretation of this still puzzling phenomenon would be the
action of weak repulsive twin matter distribution between stars, inside
galaxies, which would form, as for spiral structure, a weak potential barrier.
To be investigated.
11) The question of the repulsive power
of vacuum. An alternative answer.
...When we look to equation (29) we see
that T acts like a
"cosmological constant". It figures the "repulsive power of the
twin universe", which can play a role in non-steady coupled solutions.
Assumption of homogeneity and isotropy gives the Riemanian metrics the
well-known Robertson-Walker form, as follows :
![]()
![]()
...The radial distances between
conjugated points (same u, an non-dimensional "radial distance", with
respect to an arbitrary point) are not automatically equal :
r = R u .......................r = R
u
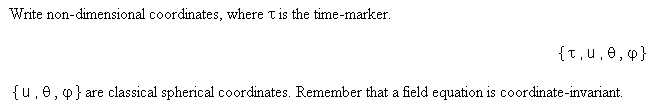
The choice of coordinates remains free, in each fold,
where we can define different cosmic times :
. t ...et ...
t

R = cT R R = c T R

...We put the field equations into
their non-dimensional forms, using :
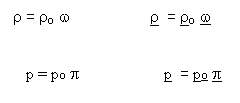
Following, these tensors,
written in their non-dimensional forms :
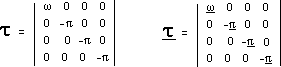
At the end, we get four
second order coupled differential equations (instead two, in the classical
approach). :

...We need some additional hypothesis. Assume that the two universes have "parallel lives" during their radiative epoch, i.e :
![]()
which impose negative curvature indexes ( k
= k = -1 ). After decoupling we neglect the pressure terms (dust
universes) :
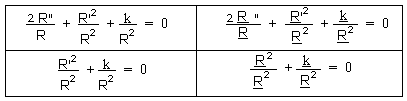
from which we get
immediately :
![]()
Introducing the
mass-conservation in both folds :
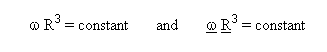
the system becomes :
![]()
...Notice that R = R gives R" = R" = 0. On another hand, if the two universes were "fully coupled",
i.e. R/R = constant, this peculiar solution would
correspond to Friedmann models, with "parallel evolutions". But we
consider that they are coupled by gravitational field, through (54-a) and
(54-b), which shows that the linear expansion is unstable. If, for an example,
if R > R then R" > 0
and R" < 0 . The
system can be numerically solved. The typical solution corresponds to figure
13. The numerical values have been chosen in order to fit the initial condition
for VLS numerical simulation. The law of evolution, for the radiative epoch
will be justified in section 15.
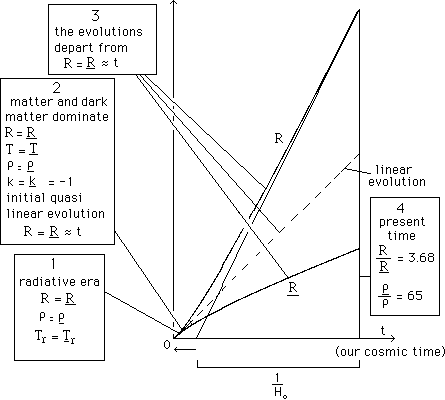
Fig.13 : The evolution of the scale parameters of the universe and twin
universe.
...We see that this system of two
universes interacting through gravitational force is unstable. If one universe
goes faster, pushed by his twin, the other one slows down. The observed
acceleration of our universe is then caused bay the "repulsive power of its
twin universe". The histories of the two differ. Ours is cooler and more
rarefied. The twin is warmer and denser. This justifies the assumption of
section 2, which determines the VLS.
...What could be the evolution of our twin
universe ? As we have seen, it is filled by huge clumps of twin matter which
look like huge proto-stars, whose cooling time is fairly larger than the age of
the universe. Fusion does not occur in the twin universe. We think after first
nucleo-synthesis, it remains filled by hydrogen and helium. Life phenomenon
would not exist in the twin universe.
12) Newton’s law and Poisson equation.
In classical General
Relativity the Newton law and the Poisson equation can be derived from Einstein
field equation, considering an almost steady state and almost Lorentzian metric
solution. Here, we have two perturbed metrics, written in non-dimensional
coordinates h(time) , z a (space)
![]()
Expanding the two field
equations into series, and considering an almost uniform universe we get
![]()
Introduce a non-dimensional
gravitational potential :
![]()
Defining a non-dimensional
Laplacian operator :
![]()
we get a non-dimensional
Poisson equation :
![]()
The classical method of
identification gives the Newton law. In fold F :
![]()
In fold F :
![]()
The gravitational potential
acts differently on a (m = +1 )
test-particle. Depends the fold it belongs to. In general a (m= +1) particle
located in fold F gives the following contribution the the (non-dimensional)
gravitational potential.
![]()
As we can see, the system
of coupled field equations determines completely the dynamics of the system,
corresponding to Newtonian approximation, as introduced as an hypothesis in the
beginning of the paper. In the model the velocities of light c and c may
be different (and we think they are). Using the dimensional quantities
introduced in section 11 we may return to dimensional laws, as following :
![]()
![]()
The Newton law, expressed
in the two folds, becomes :
![]()
The Poisson equation can be
expressed indifferently in both folds
![]()
13) Scalar curvatures.
What is the geometrical
meaning of the system (29) plus (30) ? The scalar curvatures R and R are
opposite. We may give a didactic image of this new geometrical framework.
First, remember that the structure corresponds to a two-folds cover of a
manifold. We get two distinct folds, with coupled metrics g and g. They are
note independent, for they are solution of the field equation system. They produce
their own system of geodesics and the image, in fold F, of a geodesic of
fold F is not a geodesic of that twin fold F. Light follows
null-geodesics in both folds, but no null-geodesic links the two, so that the
structure of one fold are geometrically invisible for an observer located in
the other one. Assume now a mass is present un fold F, while the adjacent
portion of fold F is empty. The corresponding field equations system
would be :

Assume this mass
distribution corresponds to a sphere with radius ro, filled by
constant density material, and surrounded by void. Then the geometry, in fold
F, is steady state is assumed, corresponds to two linked Schwarzschild
solutions (internal and external). They are solutions of equation (68). In fold
F we get a conjugated geometry,
with opposite scalar curvature R = - R. Outside the sphere (and outside
the corresponding adjacent space in fold F) R = R = 0. Inside the
scalar curvatures are constant. The didactic model corresponds to a blunt
“posicone”, associated to a “blunt negacone”, as shown on figure 15. In a blunt
“posicone” the central portion is a portion of a sphere.
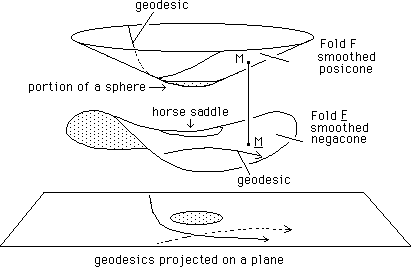
Fig.14 : A
mass is present in the fold F. Induced negative curvature in fold F
In
un “blunt negacone” the associated region corresponds, in this 2d didactic
image, to a horse saddle. Below, a plane which figures how an observer located
in fold F conceives this. He can observe both the mass M (grey disk) and the
path of a mass cruising in his fold, “attracted by this mass” , this path, in
this Euclidean representation corresponding to the projection of a geodesic of
the “blunt posicone”. The observer cannot see the path of a particle of “twin
matter”, cruising in the twin fold F and repelled by the mass.
Now,
assume the mass is located in the fold F, in the twin space. The
situations are reversed. See on figure 15. Following this 2d didactic image,
the fold F is shaped as a blunt negacone, while the fold F looks like a
blunt posicone.The geometry of F, close to the geometrical centre of the system
evokes the vicinity of a twin matter clump located at the centre of a “cell” in
the VLS. Light travelling in our fold can cross it, but it is sprayed. As
evoked in section 3 and on figure 7 it implies that the clumps’ diameters could
not be larger than a certain value, to be computed, in order to fit the
available observations. Below : two plane representations showing Euclidean
projections (how an observer could conceive the phenomenon, when located in
fold F or in fold F).
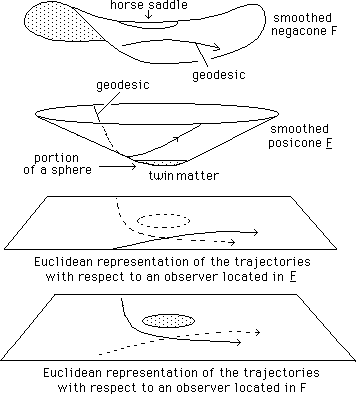
Fig.15 : A
mass of “twin matter” is present in the fold F, while the fold F is
empty.
It produces a negative (induced) curvature in F.
