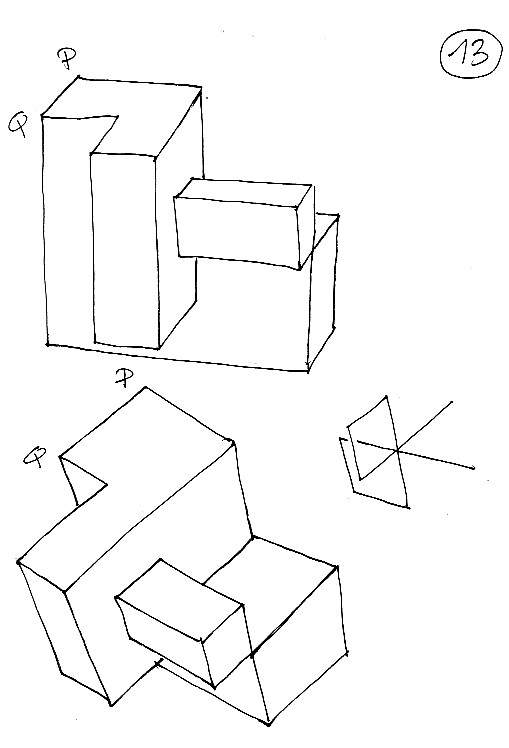
Comment transformer une crosscap en surface de Boy (droite ou gauche, au choix) en passant par la surface Romaine de Steiner.
27 septembre 2003
page 4
On présente alors le modèle sous un autre angle :

Planche 14 : On réédite la même opération en créant la troisième "oreille" de la courbe d'auto-intersection. En polyédrique celle-ci a la forme de trois carrés ayant un sommet commun : le point triple T .
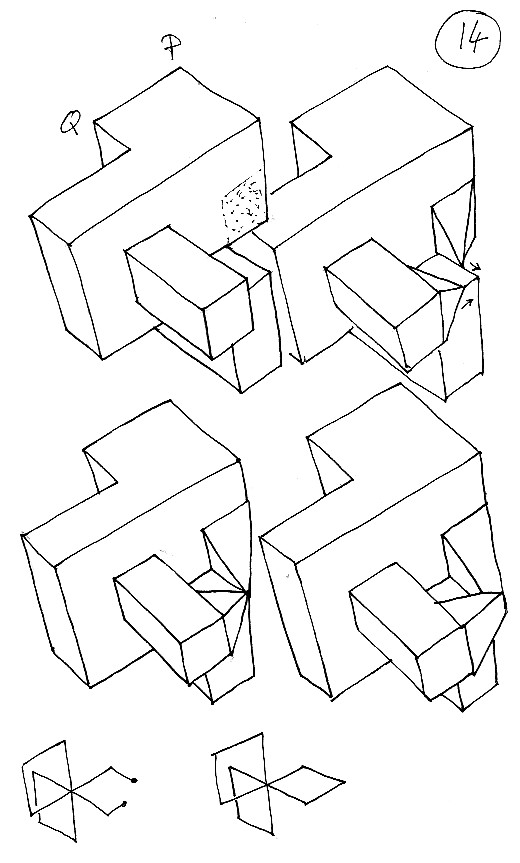
Planche 15 : en faisant tourner l'objet vous retrouvez la version polyédrique de la surface de Boy que j'avais incentée et présentée dans le Topologicon (où se trouve un découpage permettant de la construire).
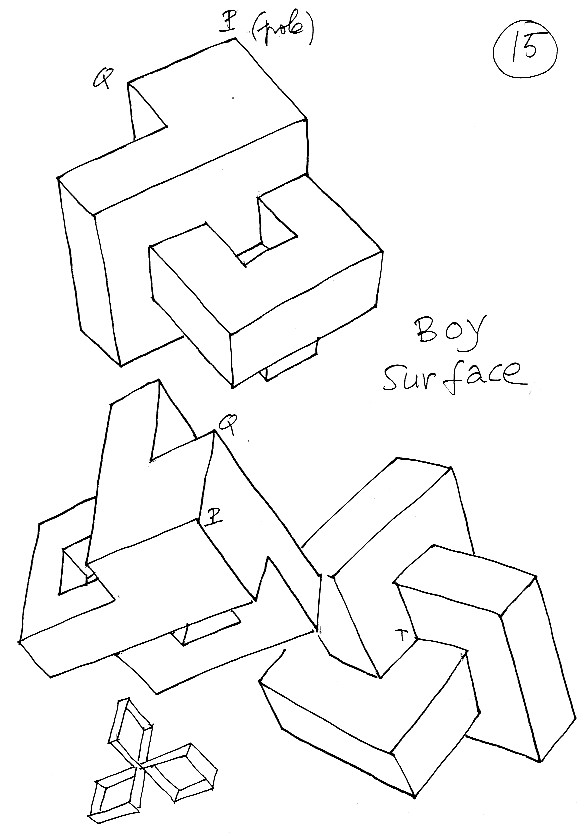
Dernière planche : j'ai essayé de figurer la surface de Steiner ( du 4° degrés, alors que la Boy est du sisxième ) en train de se contorsionner et de se transformer en surface de Boy.
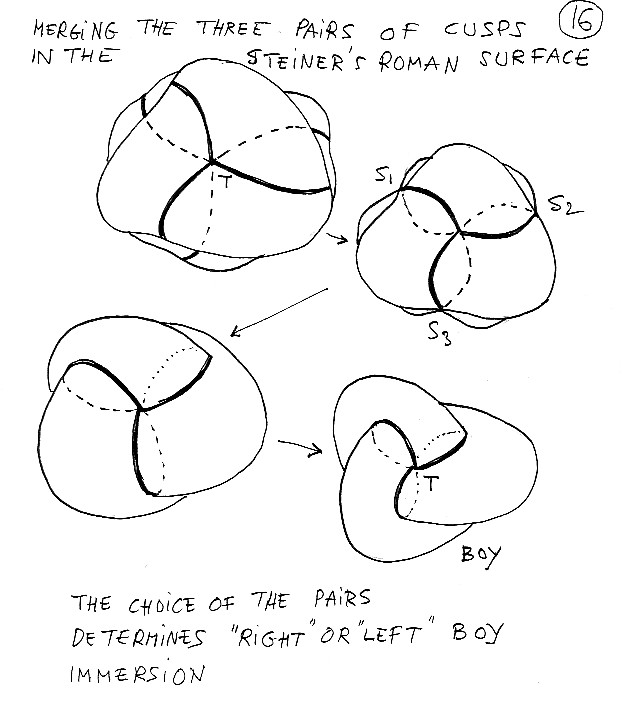
On voit qu'en "rondouillard" il faut une sacrée habitude pour comprendre l'objet. Notre oeil est très mal à l'aise lorsqu'il s'agit de comprendre un objet où, sur une même ligne de vue de supersposent plus de deux nappes. D'où l'intérêt du polyédrique qui met à portée du tout venant des transformations considérées comme sophistiquées en géométrie, dans la mesure où les gens font l'effort de construire les modèles eux-mêmes. Au passage on remarque que selon les paires de points cuspidaux choisis on obtient une surface de Boy "groite" ou "gauche" (mots totalement arbitraires). Le plan projectif s'immerge selon deux représentations "énantiomorphes", en miroir. On voit qu'on peut passer d'une Boy droite à une Boy gauche par l'intermédiaire d'un modèle "central" qui est la surface Romaine de Steiner.
Il serait sans doute sympathique que de tels dessins soient publiés dans Pour la Science ou La Recherche. Mais depuis vingt ans je suis "interdit de publication" dans ces revues pour cause de déviationisme ovniesque. Merci messieurs Hervé This et Philippe Boulanger. Je ne compte plus les articles de ce genre que j'ai envoyé à ces revues et qui m'ont été poliment retournés. On finit par se faire à son statut d'excommunié.
A titre anecdotique il existe en France un "prix d'Alembert" destiné à récompenser des auteurs de livres de vulgarisation en mathématique. L'histoire m'a été contée par un membre de la commission chargée de déterminer à qui devait revenir le prix (il y a quand même quelques sous à la clé). Dialogue :
- Mais enfin, est-ce qu'on ne pourrait pas attribuer à Petit le prix ? Il a fait des ouvrages remarquables comme le Géométricon, le Trou Noir et le Topologicon.
- Oui, mais il n'a pas fait que ces albums.
- A quoi faites-vous allusion ?
- Il a aussi écrit le Mur du Silence.
- Ah, dans ces conditions....
Eh oui, le Mur du Silence, paru en 83, est un album consacré à la MHD. Et, comme chacun sait cette science sulfureuse a pour vertu, ou pour malice de permettre aux soucoupes volantes d'évoluer à vitesse supersonique sans faire de Bang.
Cachez cette science, que je ne saurais voir
J'ai dans mes cartons une version du "retournement du cube" superbe avec un modèle central de toute beauté, qui n'est pas la version polyédrique de la variante de Morin. Le tout de mon cru. Un de ces quatre.....
22 octobre 2003 : On ne se bouscule pas sur ces pages, si j'en crois le chiffre du compteur. J'ai donné le lundi 13 octobre 2003 un séminaire au CMI (Centre de mathématiques et d'informatique de Château-Gombert-Marseille) sur invitation de Trotman. A l'occasion j'ai pu aligner une collection d'une trentaine de modèles en carton, dont vous aurez un jour prochain la primeur, ceux-ci ayant été photographiés par Christophe Tardy.
Quand on donne un séminaire, une ambiance se dégage. Sur la photo suivante, un géomètre qui exprime sa perplexité.

En arrière plan, une partie des modèles exposés. A un moment j'ai posé la question :
- Quels sont ceux qui ont déjà vu une surface Romaine de Steiner ? Levez la main.
Personne n'en avait jamais vu. J'ai donc jugé utile de présenter l'objet, en réalité virtuelle, sur le portable que j'avais amené, objet réalisé avec le concours de Christophe Tardy, ingénieur et de Frédéric Descamp, de L'Institut Laue Langevin de Grenoble (ILL). Visiblement cette présentation déconcerte l'assistance, peu habituée à voir les surface mathématiques virevolter à volonté.

Deux panneaux de carton, visibles en premier plan, avait permis de présenter la suite des modèles dans leur ordre logique. Les modèles "vert et jaune" illustrent, en polyédrique, l'outil essentiel de création-décréation d'une paire de points cuspidaux. L'objet blanc le plus distant est une version polyédrique de la Cross Cap, qui se transforme d'abord en version polyédrique de la surface Romaine de Steiner, un mètre plus loin puis, à volonté, en surface de Boy "droite" ou "gauche".
L'analyse des maquettes fait émerger différentes remarques dans l'assistance. Un des géomètres demande :
- Si, en suivant les maquette dans ce sens, on peut passer de la Cross Cap à la Boy il semble qu'en faisant l'inverse on doit pouvoir transformer une Boy en Cross Cap.
Je réponds par l'affirmative. Enhardi, mon interloculeur ajoute :
- Si, en arrivant au stade de la surface Romaine de Steiner on s'arrête, il devient alors possible de reprendre vers une surface de Boy en miroir.
J'approuve une seconde fois. Mais hélas personne ne se proposera pour donner des éclaircissements sur ce monde étrange où on dote des immersions de surfaces fermées des points cuspidaux, créés ou annihilés par paires, l'ensemble constituant une sorte d'extension du monde des immersions. Le mot "submersions" me paraîtrait seyant. Si un lecteur met la main sur des éclaircissements, ils seront les bienvenus.
Courbure concentrée en un point cuspidal
On la calculera en sommant les angles au sommet et en comporant cette somme à la somme euclidienne : 2 p .
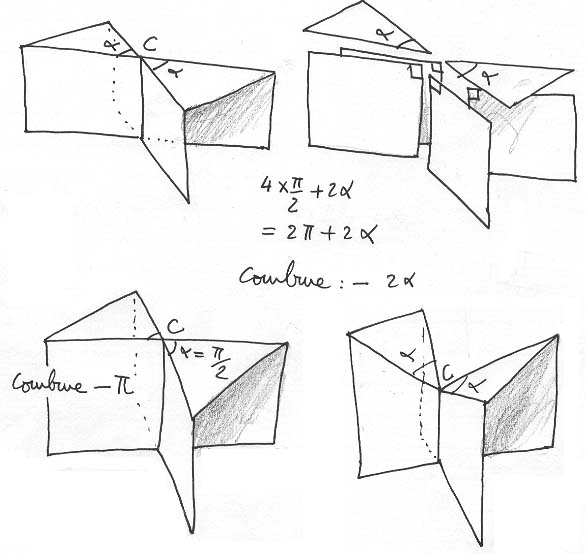
En haut et à gauche on a fait figurer une des multiples représentations polyédriques du point cuspidal. Le "démontage" de l'objet (à droite) conduit à une somme excédant la somme euclidienne 2 p d'une valeur 2 a . On en déduire que la courbure angulaire concentrée au voisinage de ce point C est - 2 a. Si l'angle a est égal à p/2 alors la courbure négative vaut c (figure en bas et à gauche). En fait la courbure concentrée en un point cuspidal peut prendre une infinité de valeurs. En bas et à droite on accentue la somme angulaire et la courbure devant alors < 2 a. On accentue la courbure négative.
En opérant de manière inverse on peut déboucher sur une situation assez étonnante : faire en sorte que la courbure (angulaire) concentrée en C soit ... nulle :
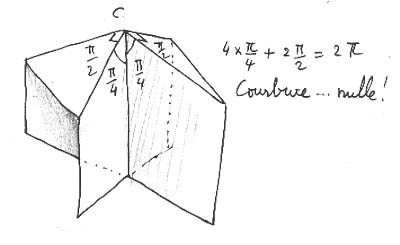
On peut partir maintenant d'une représentation polyédrique de la Crosscap où figurent deux points cuspidaux correspondant chacun à une courbure négative égale à - p :
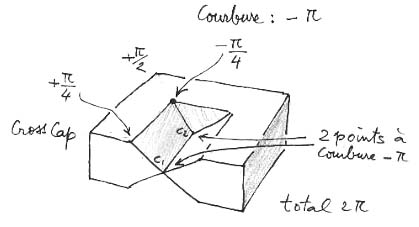
Il y a huit "posicoins" correspondant à une valeur + p/2. Ajoutons quatre autres "posicoins" de courbure + p/4 et quatre "négacoins de courbure - p/4
Plus les deux points cuspidaux de coubure - p .
Total : 2 p
En divisant cette courbure totale par 2 p on retrouve la caractéristique d'Euler-Poincaré de toutes les représentations du plan projectifs (comme la surface de Boy).
Au cours de ma conférence j'ai évoqué l'art et la manière de permuter les deux points cuspidaux d'une Cross Cap, en utilisant le retournement de la sphère. Je ne sais plus si j'ai mis cela quelque part dans mon site. C'est un tel fouillis. Il faudra que je cherche, sinon je mettrai cela quelque part. C'est assez amusant. Toujours est-il que cette prestation ne plut guère à un des présent, lors du séminaire.
- Je ne vois pas pourquoi Petit fait usage d'un tel attirail pour démontrer la symétrie qui unit les deux points cuspidaux d'une Cross Cap. Il y a beaucoup plus simple.
Et il traça au tableau l'image d'une sphère écrasée par deux réglettes qu'on rend jointives et qui donne effectivement un ensemble d'auto-intersection sous la forme d'un segment bordé par deux points cuspidaux, comme c'est le cas de la Cross Cap. Hélas, et notre homme s'en aperçut, ça n'est pas une Cross Cap.
- Diantre, mais alors qu'est-ce ? Demanda quelqu'un.
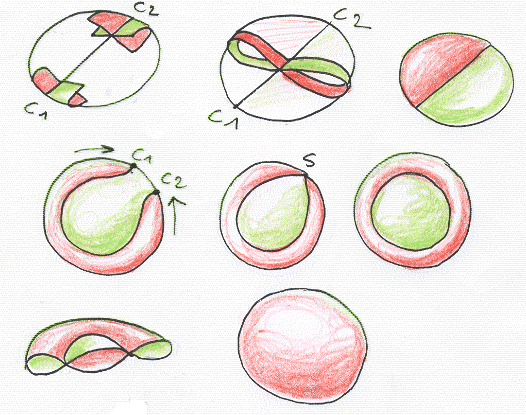
C'est tout simplement une sphère, muni de deux points cuspidaux. Si on les fait confluer on obtient une ligne d'auto-intersection qui devient alors un simple cercle. Et on obtient en bas et à gauche (en coupe) une immersion de la sphère qu'on a plus qu'à transformer en son plongement. On peut en outre passer à une représentation polyédrique de cette surface :
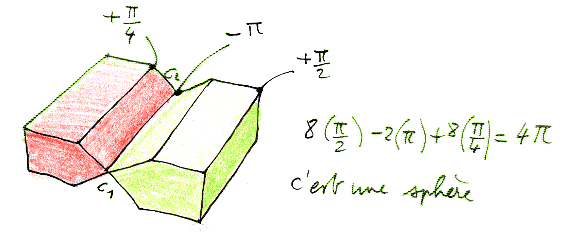
C'est bilatère et la courbure est 2 p.
On peut donc s'amuser pas mal avec ces "submersions". Prenons une immersion du tore qui consiste à faire tourner le signe "infini" ou un "huit", autour d'un axe.
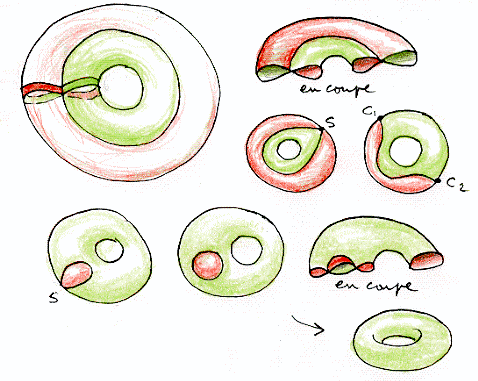
La technique de confluence des points cuspidaux nous permettra d'arriver très rapidement au plongement standard du tore, comme indiqué dans la suite des dessins.
Mais les choses ne s'avèrent parfois pas aussi faciles et évidentes. Je prends par exemple une sphère que j'écrase entre deux segments qui, cette fois, ont des longueurs inférieures au diamètre. On obtient encore deux points cuspidaux.
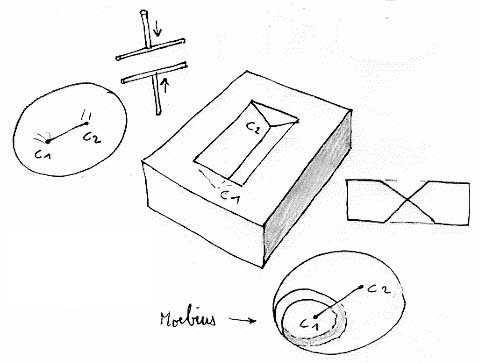
Comme on peut y inscrire un ruban de Moebius cette surface est unilatère. On a fait figurer sa représentation polyédrique qui permet de calculer sa courbure totale. On trouve alors zéro. Si je ne m'abuse ce serait alors une bouteille de Klein. On ne connait en général que l'immersion la plus classique où la ligne d'auto-intersection est un simple cercle. Mais il y en a d'autres, comme celle-ci. J'avoue que je n'ai pas encore trouvé comment transformer l'objet ci-dessus en une immersion de la bouteille de Klein. Je ne sais d'ailleurs si les différentes immersions relèvent du même groupe d'homotopie (la sphère n'en a qu'un). A priori non, puisque le tore peut être immergé de quatre manières différentes, qu'on ne peut relier entre elles par une homotopie régulière. En attendant je me suis amusé à transformer cette surface en créant deux points cuspidaux supplémentaires et on obtioent alors Deux Cross Caps reliées par un tube. En les découposant on retrouve une caractéristique d'Euler Poincaré égale à zéro.
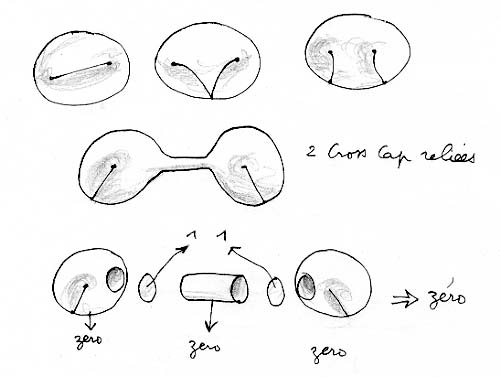
Cette "surface bizarre" devrait pouvoir se transformer en une des immersions de la bouteille de Klein. Mais laquelle ? En tout cas en voici une obtenue en faisant tourner le "Huit" autour d'un axe et en en lui faisant opérer en prime un demi-tour :

Retour au sommaire " Transformation d'une Cross Cap en Boy "
Retour vers Nouveautés Retour vers Guide Retour vers Page d'Accueil
Nombre de consultations depuis le 6 octobre 2003 :