30 décembre 2009
J'ai vendu la surface de Boy que j'avais créée

Ca y est : cet objet d'un mètre quarante d'envergure est parti ce matin pour la Belgique, acheté par un médecin, Pierre par ailleurs fidèle lecteur des bandes dessinées de Lanturlu et connaissant déjà l'objet par la lecture de l'album le Topologicon, gratuitement téléchargeable sur le site de Savoir sans Frontières à :
http://www.savoir-sans-frontieres.com/JPP/telechargeables/Francais/topologicon.htm
Le Topologicon est cité dans la page de Wikipedia, mais le lien ne conduit pas à la page de téléchargement du Site Savoir sans Frontières, ce qui est assez dommage. Quelqu'un pourra peut-être rajouter ce lien, mais je saurais personnellement le faire, ayant été " banni à vie " de Wikipedia en octobre 2006 ( pour avoir dévoilà l'identité d'un contributeur, ancien élève de Normale Supérieure, à qui son doctorat ès science en physique théorique, sur les supercordes, permit d'accéder à un poste dans une banque ).
Cet objet a été exposé pendant vingt cinq ans dans la " salle pi " du Palais de la Découverte de Paris. Je l'avais récupéré il y a quelques années à l'époque où la direction du Palais avait voulu installer dans cette salle un mini amphi en bois. J'ai préféré le récupérer, avant qu'il ne finisse écrasé, entreposé dans quelque réserve, au titre d'une " science consommable ".
Quand s'était tenu au Palais une exposition consacrée aux différentes théories concernant la construction des pyramides, les ateliers avaient réalisé une assez jolie maquette, de 50 cm sur 50 cm, montrant les pièces d'angle de ma rampe en pierre. J'ai souhaité récupérer l'objet, mais aux dernières nouvelles il a été perdu. A moins qu'en tant que consommable scientifique il ait fini dans une poubelle. Peut être un lecteur pourra-t-il me renseigner ?
Quand on visite la Cité des Science on est frappé par l'invasion du virtuel, des écrans à plasma montrant ceci ou cela. Au point qu'on est tenté de se dire : " pourquoi me rendre en ces lieux, alors que je peux tout aussi bien avoir accès à cela chez moi, grâce à Internet ? "
Mondes virtuels, sciences consommables, avez-vous donc une âme ?
C'est dans l'air du temps.
En quoi la surface de Boy est-elle importante en mathématiques ? Au rayon des surfaces fermées à deux dimensions, exemptes de points singuliers, on n'en trouve que quatre :
- La sphère - Le tore - La bouteille de Klein - La surface de Boy |
Les trois premières nous étaient familières de longue date. La quatrième était plus mystérieuse. Ca n'est qu'à la fin des années soixante-dix, lorsque j'étais professeur de sculpture à l'Ecole des Beaux Arts d'Aix en Provence, que j'ai construit la première représentation de cette surface, avec deux familles de courbes, équivalant aux ensembles méridiens-parallèles de la sphère S2. Comme on le verra dans la bande dessinée, la surface inventée par le mathématicien allemand Werner Boy, élève de Hilbert, est le résultat de l'application des points d'une sphère les uns sur les autres, chaque point étant mis en coincidence avec son antipode. Ainsi le pôle nord est-il amené en coincidence avec le pôle sud. Les méridiens de la sphère " s'enroulent sur les méridiens de la Boy".
J'ai immédiatement eu l'idée d'identifier une des familles de courbes avec des ellipses.
A l'époque le jeune Jérôme Souriau pouvait utiliser l'Apple II de son mathématicien de père. Un jour je lui dis :
- Voudrais-tu faire pour moi un travail qui nous vaudrait une publication dans le domaine des mathématiques ?
Et Jérôme de répondre :
- Qui dois-je tuer pour cela ?
Il s'agissait simplement d'effectuer des mesures sur les ellipses, à l'aide d'un rapporteur et d'une règle graduée, afin de construire des courbes, puis leur représentation à l'ide d'une série de Fourier. Il réalisa le travail en un après-midi. La note aux comptes rendus de l'Académie des Sciences de Paris passa sans difficulté. Voir cette reproduction de la note
Ces équations permirent à Colonna, dirigeant le premier atelier d'images de synthèse de l'Ecole Polytechnique de Paris de produire les premières images de l'objet, mais sans mentionner les équations qu'il avait utilisées pour faire ce travail (comportement assez courant dans la " communauté chientifique" ).
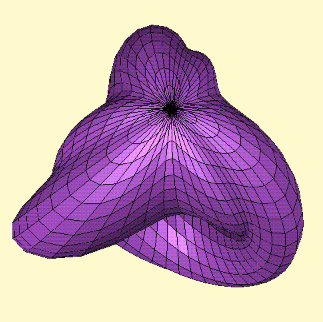
Image créée à partir de la représentation JP PETIT - Jérôme Souriau, avec ses trois vilains plis,
issus d'un manque de finition dans la représentation de Fourier.
Par la suite les représentations paramétriques se multiplièrent. Ci-après, celle de R.Bryant :


Cette seconde découverte, celle d'une paramétrisation à l'aide de méridiens elliptiques permit au mathématicien Apéry, élève du mathématicien Bernard Morin, de Strasbourg, de construire la première représentation de la surface sous une forme implicite, du sixième degré.( dans sa thèse de doctorat il attrubue cette invention au plasticien Max Sauze, docteur ès soudures à l'argent) :
f(x,y,z) = 64 (1 - z)3 z3 - 48 (1 - z)2 z2 (3x2 + 3y2 + 2z2) + 12 (1 - z) z (27 (x2 + y2)2 - 24 z2 (x2 + y2) + 36 Sqrt(2) y z (y2 - 3 x2) + 4z4) + (9x2 + 9y2 - 2z2) (-81 (x2 + y2)2 - 72 z2 (x2 + y2) + 108 Sqrt(2) x z (x2 - 3y2) + 4z4) = 0
effroyablement compliqué.

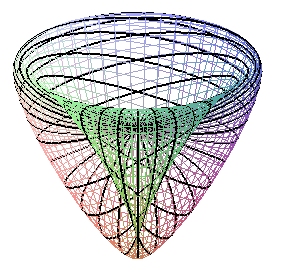
Image de la surface de Boy, construite à l'aide de la représentation implicite d'Apéry, avec les " méridiens elliptiques " de J.P.Petit
Sur le site de Wikipedia, à cette page, on trouvera une animation, inspirée par le flip book qu'on trouvera dans le Topologicon (1988). Même chose pour la représentation polyédrique de la surface (autre invention de votre serviteur, également présente dans l'album), aux angles émoussés.
En 1988 le mathématicien Brehm a donné une autre représentation polyédrique, à dix faces et un théorème indique que l'objet ne saurait avoir moins de 9 faces....
de gustibus et coloribus non disputandum
Revenons à la représentation d'Apéry, seule représentation implicite connue. Pourquoi cette surface est-elle si disharmonieuse ( et donc son équation si compliquée ) ?
Apéry, guidé par Morin, n'a pas exploité la symétrie ternaire de l'objet. L'équation place l'axe OZ comme axe de symétrie; ce qui est une erreur. Un meilleur résultat aurait été obtenu en choisissant comme axe de symétrie le vecteur ( 1 , 1 , 1 ). La symétrie ternaire aurait alors donné une équation invariante en permutant les coordonnées x , y , z . Qui plus est, en plaçant l'origine des coordonnées au point triple et en décidant que les trois plans tangents à la surface sont les plans principaux, on éliminerait les termes d'ordre deux, un et zero, et on réduirait le terme d'ordre trois à
x y z
Une telle symétrie est exploitée dans la surface découverte en 1844 Par Steiner, dans la ville de Rome, appelée par la suite la surface Romaine de Steiner, dont l'équation est :
![]()
Coup d'oeil à la surface :

La surface romaine de Steiner
Constituée également par des ellipses, elle est, comme cette dernière, unilatère, donc incomestible. :
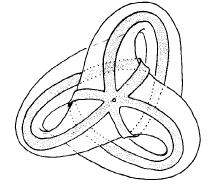
Les familles d'ellipses de la surface romaine
La surface romaine n'est " ni droite, ni gauche ", alors qu'il existe deux versions de la Boy, énantiomorphes, en mriroir. Une Boy " droite" et une Boy " gauche ". En 2003 (que le temps passe vite ) j'avais montré, lors d'un séminaire donné au département de géométrie de la face de Saint Jérôme de Marseille qu'on pouvait transformer une Boy droite en Boy gauche en passant par une surface romaine de Steiner.
http://www.jp-petit.org/science/maths_f/Crosscap_Boy1.htm

L'auteur donnant un séminaire en maths.
Certain lecteurs manient bien les outils infographiques. En suivant le dossier indiqué, en numérisant et en interpolant il est possible de constituer l'animation. Si cela tente quelqu'un .....
C'est amusant, les animations. J'avais constitué celle-ci avec le logiciel de CAO que j'avais créé : Screen et qui représente l'étape centrale du retournement du cube ( alias version poilyédriques du modèle à quatre oreilles de Morin )
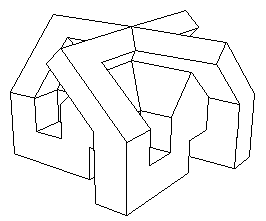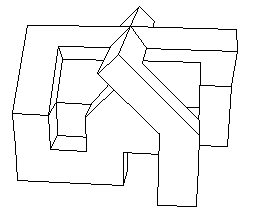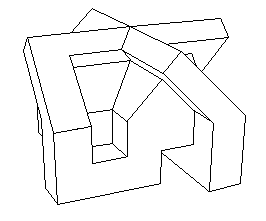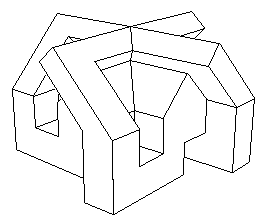
L'étape centrale du retournements du cube
Il y en aurait, des choses à faire, dans ce domaine. Je voudrais simplement indiquer une piste pour candidats thésards en thèse de maths. Il existe une représentation implicite de la surface de Boy dont les méridiens sont des ellipses et c'est cette équation qui s'inscrira dans l'histoire des mathématiques, ainsi que le nom de celui qui la dégagera de sa gangue. Elle reste à trouver. Point de départ : exploiter la symétrie ternaire comme indiqué plus haut.
Bonne chasse....
Ainsi la surface de Boy qui avait orné la salle pi du Palais de la Découverte est partie en Belgique. J'aurais bien aimé qu'on en tire une sculpture monumentale, " pénétrable " , de vingt mètres de haut. Ca, au moins, ça aurait eu de la gueule. Mais non, des plasticiens de bazar ont peuplé cet espace de sculptures sans âmes, sans structures, dénuées de la moindre richesse.
Mais je n'ai pas voulu garder de photo de cet objet fantastique. On comprendra pourquoi
Nouveautés Guide ( Index ) Page d'accueil